题目内容
11个连续两位数乘积的末4位都是0,那么这11个数的总和最小是多少?
考点:最大与最小
专题:传统应用题专题
分析:连续两位数乘积的末4位都是0,因10000=2×2×2×2×5×5×5×5,也就是说这11个数里要含有4个因数5,但是连续11个数有最多只能有3个数是5的倍数,所以其中一个数是25的倍数,要求11个数总和最小,要把25放在最后1个数这样这11个数是15,16,17,18,19,20,21,22,23,24,25.据此解答.
解答:
解:要使11个连续两位数乘积的末4位都是0,则这11个数里要有4个因数5,要使这11个数的和最小,则满足条件的最大两位数是25.所以和最小是:
15+16+17+18+19+20+21+22+23+24+25
=(15+25)×11÷2
=40×11÷2
=220
答:这11个数的总和最小是220.
15+16+17+18+19+20+21+22+23+24+25
=(15+25)×11÷2
=40×11÷2
=220
答:这11个数的总和最小是220.
点评:本题的关键是根据乘积的末4位是0,确定因数中有几个5,再确定最大的数是25,然后解答即可.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 将1至12这12个自然数填入如图的“灯笼”中,使得四个椭圆和两条竖线上的各数之和均相等.这个和数最大是多少?请给出一种填法.
将1至12这12个自然数填入如图的“灯笼”中,使得四个椭圆和两条竖线上的各数之和均相等.这个和数最大是多少?请给出一种填法. 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2厘米和4厘米,乙三角形两条直角边分别为3厘米和6厘米,求图中阴影部分的面积.
按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2厘米和4厘米,乙三角形两条直角边分别为3厘米和6厘米,求图中阴影部分的面积.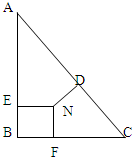 如图在直角三角形ABC中,AB⊥BC,ND⊥AC,NE⊥AB,NF⊥BC.四边形BFNE是正方形,AB=4,BC=3,AC=5,ND=1,则正方形BFNE的边长等于
如图在直角三角形ABC中,AB⊥BC,ND⊥AC,NE⊥AB,NF⊥BC.四边形BFNE是正方形,AB=4,BC=3,AC=5,ND=1,则正方形BFNE的边长等于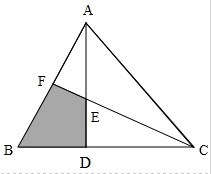 已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.
已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.