题目内容
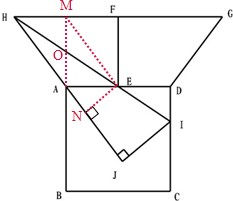
 如图,ABCD是长边为6的正方形,ADGH是一个梯形,点E、F分别是AD、GH的中点,HF=6,EF=4,EF⊥GH.联结HE并延长交CD于点I,作IJ⊥HA,则IJ=
如图,ABCD是长边为6的正方形,ADGH是一个梯形,点E、F分别是AD、GH的中点,HF=6,EF=4,EF⊥GH.联结HE并延长交CD于点I,作IJ⊥HA,则IJ=考点:三角形的周长和面积,长方形、正方形的面积,梯形的面积
专题:平面图形的认识与计算
分析:如下图所示作辅助线,过点E作EN⊥HJ于点N,延长BA,交EH于点O,交HG于点M,则AM⊥HF,AM⊥AD,因此AM=EF=4;由点E、F分别是AD、GH的中点,可知AE=HM=3,又HM∥AE,所以四边形AEMH是平行四边形,则OA=
AM=
×4=2,由△OAE≌△IDE,可得DI=AO=2;在RT△AMH中,由勾股定理可得AH=5;同理可得HE=2
,EI=
,于是可以求得HI=HE+EI=3
;由S△HAE=
AE?EF=
AH×EN,可以求得EN的长;由∠ENJ=∠J=90°,∠NHE=∠JHI,可得△HNE∽△HJI,由相似三角形的对应边成比例即可求得IJ的长.
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 13 |
| 13 |
| 1 |
| 2 |
| 1 |
| 2 |

解答:
解:如图作辅助线,由分析可知,
AM⊥HF,AM⊥AD,则AM=EF=4;
因为点E、F分别是AD、GH的中点,
所以AE=HM=3,
又HM∥AE,
所以四边形AEMH是平行四边形,
所以OA=
AM=
×4=2.
因为AE=DE,∠AEO=∠DEI,∠OAE=∠IDE=90°,
所以△OAE≌△IDE,
所以DI=AO=2;
在RT△AMH中,由勾股定理可得AH=
=5,
同理可得:HE=2
,EI=
,
所以HI=HE+EI=3
;
由S△HAE=
AE?EF=
AH×EN可得:
×3×4=
×5×EN,
解之得,EN=2.4;
因为∠ENJ=∠J=90°,∠NHE=∠JHI,
所以△HNE∽△HJI,
所以
=
,
所以
=
,
解得IJ=3.6.
故答案为:3.6.
AM⊥HF,AM⊥AD,则AM=EF=4;
因为点E、F分别是AD、GH的中点,
所以AE=HM=3,
又HM∥AE,
所以四边形AEMH是平行四边形,
所以OA=
| 1 |
| 2 |
| 1 |
| 2 |
因为AE=DE,∠AEO=∠DEI,∠OAE=∠IDE=90°,
所以△OAE≌△IDE,
所以DI=AO=2;
在RT△AMH中,由勾股定理可得AH=
| 32+42 |
同理可得:HE=2
| 13 |
| 13 |
所以HI=HE+EI=3
| 13 |
由S△HAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解之得,EN=2.4;
因为∠ENJ=∠J=90°,∠NHE=∠JHI,
所以△HNE∽△HJI,
所以
| HE |
| HI |
| EN |
| IJ |
所以
2
| ||
3
|
| 2.4 |
| IJ |
解得IJ=3.6.
故答案为:3.6.
点评:本题较难,辅助线很关键;用到平行四边形的判定以及性质,三角形的全等及相似,勾股定理等知识.

练习册系列答案
相关题目
从左边看下面的两个图形的形状正确的分别是( )


A、 |
B、 |
C、 |
一个小数的小数点向左移动三位,向右移动两位,所得到的这个数比原数( )
| A、扩大100倍 |
| B、扩大10倍 |
| C、缩小10倍 |
| D、缩小100倍 |
