题目内容
如图所示,场源O处有一正电荷,一电子在电场、磁场中做匀速圆周运动(不计重力).某时刻电场消失,电子仍在磁场中运动的速度v、半径r、周期T的可以情况是( )
 |
试题答案
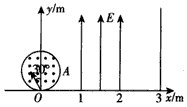
D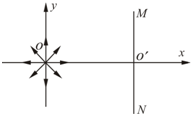 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右侧有一很薄的挡板,垂直于x轴放置,挡板与xoy平面交线的两端M、N正好与原点O构成等边三角形,O′为挡板与x轴的交点.在整个空间中,有垂直于xoy平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动.已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN的长度为L.(不计带电粒子的重力及粒子间的相互作用)
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右侧有一很薄的挡板,垂直于x轴放置,挡板与xoy平面交线的两端M、N正好与原点O构成等边三角形,O′为挡板与x轴的交点.在整个空间中,有垂直于xoy平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动.已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN的长度为L.(不计带电粒子的重力及粒子间的相互作用)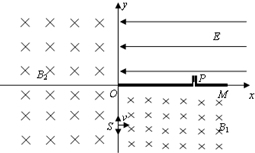 如图所示,在xOy平面的第一象限内,分布有沿x轴负方向的场强E=
如图所示,在xOy平面的第一象限内,分布有沿x轴负方向的场强E=| 4 |
| 3 |
| 3 |
| q |
| m |
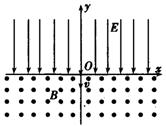
如图所示,在x轴上方存在着沿y轴负方向的匀强电场,电场强度为E,在x轴下方有一垂直纸面向外的匀强磁场,磁感应强度为B。现在坐标原点O处有一正离子源,沿y轴负方向发射比荷均为c的正离子。由于正离子的初速度不同,它们速度第一次为零时的位置不同,所需时间也不一样。
(1)写出正离子从坐标原点到速度第一次为零,所需时间与初速度关系的表达式;
(2)求具有不同初速度的正离子速度第一次为零的位置构成的曲线方程,并指出是什么曲线。
如图所示,平行板电容器MN竖直放置,极板长为L,两板间的距离也等于L。由离子源产生的带正电粒子的比荷q/m=1.0×1010C/Kg,以v0=1.0×106m/s的速度从板间的某处竖直向上进入平行板,在两板之间加一个适当的偏转电压U,可使粒子恰好从N板的边缘处飞出,且粒子的速度大小变为v=2.0×106m/s,不计粒子的重力,求:[ ]
【小题1】偏转电压U多大?[ ]
【小题2】以N板的边缘为原点,建立图示的坐标系xoy,在y轴右侧有一个圆心位于x轴、半径r=0.01m的圆形磁场区域,磁感应强度B=0.01T,方向垂直纸面向外,有一垂直于x轴的面积足够大的竖直荧光屏PQ置于某处。若圆形磁场可沿x轴移动,圆心O’在x轴上的移动范围为[0.01m,+∞],发现粒子打在荧光屏上方最远点的位置为y=2 cm,求粒子打在荧光屏下方最远点的位置坐标。
cm,求粒子打在荧光屏下方最远点的位置坐标。
如图所示,在直角坐标系的原点O 处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右侧有一很薄的挡板,垂直于x 轴放置,挡板与xoy 平面交线的两端M、N 正好与原点O 构成等边三角形,O′ 为挡板与x 轴的交点。在整个空间中,有垂直于xoy 平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动。已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN 的长度为L。(不计带电粒子的重力及粒子间的相互作用)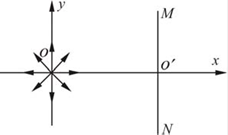
(1)确定带电粒子的电性;
(2)要使带电粒子不打在挡板上,求磁感应强度的最小值;
(3)要使MN 的右侧都有粒子打到,求磁感应强度的最大值。(计算过程中,要求画出各临界状态的轨迹图)
如图所示,在直角坐标系的原点O 处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右侧有一很薄的挡板,垂直于x 轴放置,挡板与xoy 平面交线的两端M、N 正好与原点O 构成等边三角形,O′ 为挡板与x 轴的交点。在整个空间中,有垂直于xoy 平面向外的匀强磁场(图中未画出),带电粒子在磁场中沿顺时针方向做匀速圆周运动。已知带电粒子的质量为m,带电荷量大小为q,速度大小为υ,MN 的长度为L。(不计带电粒子的重力及粒子间的相互作用)

(1)确定带电粒子的电性;
(2)要使带电粒子不打在挡板上,求磁感应强度的最小值;
(3)要使MN 的右侧都有粒子打到,求磁感应强度的最大值。(计算过程中,要求画出各临界状态的轨迹图)
查看习题详情和答案>>
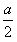 范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内。已知粒子在磁场中做圆周运动的半径介于a/2到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的
范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内。已知粒子在磁场中做圆周运动的半径介于a/2到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的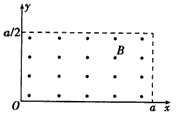

(1)当加速电场极板电压U=U0,求离子进入磁场中做圆周运动的半径R;
(2)在OQ上有一点P,P点到O点距离为L,当加速电场极板电压U取哪些值时,才能保证离子通过P点?
查看习题详情和答案>> 查看习题详情和答案>>
查看习题详情和答案>>