7. 已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与椭圆相交于点P和点Q,且OP⊥OQ,|PQ|= ,求椭圆方程.
,求椭圆方程.
解:设椭圆方程为mx2+ny2=1(m>0,n>0),
设P(x1,y1),Q(x2,y2),解方程组
 y=x+1,
y=x+1,
mx2+ny2=1.
消去y,整理得(m+n)x2+2nx+n-1=0.
Δ=4n2-4(m+n)(n-1)>0,即m+n-mn>0,OP⊥OQ x1x2+y1y2=0,
x1x2+y1y2=0,
即x1x2+(x1+1)(x2+1)=0,2x1x2+(x1+x2)+1=0,∴ -
- +1=0.
+1=0.
∴m+n=2. ①
由弦长公式得2· =(
=( )2,将m+n=2代入,得m·n=
)2,将m+n=2代入,得m·n= . ②
. ②

|
|
 m=
m= , m=
, m= ,
,
n= n=
n= .
.
∴椭圆方程为 +
+ y2=1或
y2=1或 x2+
x2+ =1.
=1.
 +
+ =1; 6.
=1; 6. 
 , AB∥PO,ΔOPF1∽ΔABO
, AB∥PO,ΔOPF1∽ΔABO  =
=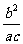 . b=c. ∴e=
. b=c. ∴e= =
= =
= .
. 是圆
是圆 为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.  ;
;  +
+ =1(a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为____________.
=1(a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为____________.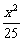 +
+ =1上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标是____________.
=1上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标是____________. B.
B. C.
C. D.
D.
 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点 为P,则
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点 为P,则 = ( )
= ( ) B.
B. C.
C. D.4
D.4