1 在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
(A) tanAtanB>1 (B) tanAtanB>1 (C) tanAtanB =1 (D)不确定
解:在△ABC中 ∵ÐC>90° ∴A, B为锐角 即tanA>0, tanB>0
又tanC<0 于是:tanC
= -tan(A+B) =  <0
<0
∴1 - tanAtanB>0 即:tanAtanB<1
又解:在△ABC中 ∵ÐC>90° ∴C必在以AB为直径的⊙O内(如图)

|
设CD = h,C’D = h’,AD = p,BD = q,
|
|
|

2.设a,bÎ( ,
, ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程 的两个根,求 a + b
的两个根,求 a + b
解:由韦达定理: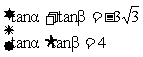
∴
又由a,bÎ( ,
, )且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
)且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
得a + bÎ (-p, 0) ∴a + b = 

 =右边
=右边 )
) =左边
=左边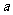 ,sinβ+cosβ=b,则
,sinβ+cosβ=b,则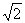 sin(α+
sin(α+
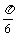 ,求x的值
,求x的值 ∵tana=3x,tanb=3-x
∵tana=3x,tanb=3-x
 即:
即:
 (舍去)
∴
(舍去)
∴


 ∴
∴ ∴a-b=
∴a-b=
 的两个实根,求tan(a+b)的取值范围
的两个实根,求tan(a+b)的取值范围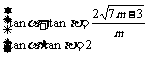 ∴
∴
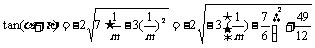
 ≤m≤2
≤m≤2 时,
时, 有最大值
有最大值
 或
或 时,
时,

 ,求f (x)=
,求f (x)=




 ,
, 时 f (x)min=
时 f (x)min=
 ,
, 时 f (x)max=2
时 f (x)max=2 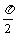 ]时,
]时, sin2x+
sin2x+





 )2-
)2-



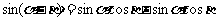


 ,设
,设
 ,数列
,数列 。
。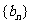 是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围.
 中,
中, 所对的边分别为
所对的边分别为 ,
, ,
, .
. ; (2)若
; (2)若 ,求
,求 。
。 集合
集合 ,
, ,且
,且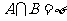
 的取值范围;
的取值范围;
 ,且
,且 ,试求实数
,试求实数 有且只有一个为真命题.
有且只有一个为真命题. 的一系列对应值如下表:
的一系列对应值如下表: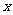
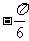










 的一个解析式;
的一个解析式;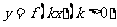 周期为
周期为 ,当
,当 时,方程
时,方程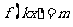 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围;
的取值范围;