1.几种终边在特殊位置时对应角的集合为:
|
角的终边所在位置 |
角的集合 |
|
X轴正半轴 |
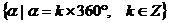 |
|
Y轴正半轴 |
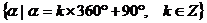 |
|
X轴负半轴 |
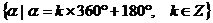 |
|
Y轴负半轴 |
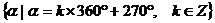 |
|
X轴 |
 |
|
Y轴 |
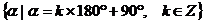 |
|
坐标轴 |
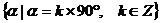 |
1.几种终边在特殊位置时对应角的集合为:
|
角的终边所在位置 |
角的集合 |
|
X轴正半轴 |
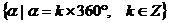 |
|
Y轴正半轴 |
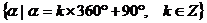 |
|
X轴负半轴 |
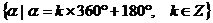 |
|
Y轴负半轴 |
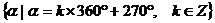 |
|
X轴 |
 |
|
Y轴 |
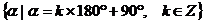 |
|
坐标轴 |
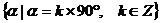 |