18.(文)(本小题满分12分)已知sin(π-α)=,α∈(0,).
(1)求sin2α-cos2的值;
(2)求函数f(x)=cosαsin2x-cos2x的单调递增区间.
解:∵sin(π-α)=,∴sinα=.
又∵α∈(0,),∴cosα=.
(1)sin2α-cos2
=2sinαcosα-
=2××-
=.
(2)f(x)=×sin2x-cos2x
=sin(2x-).
令2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+π,k∈Z.
∴函数f(x)的单调递增区间为[kπ-,kπ+π],k∈Z.
(理)(本小题满分12分)已知函数f(x)=2sinxcosx+(2cos2x-1).
(1)将函数f(x)化为Asin(ωx+φ)(ω>0,|φ|<)的形式,填写下表,并画出函数f(x)在区间[-π,π]上的图象;
|
x |
|
|
|
|
|
|
ωx+φ |
0 |
|
π |
π |
2π |
|
f(x) |
|
|
|
|
|

(2)求函数f(x)的单调减区间.
解:(1)f(x)=2sinxcosx+(2cos2x-1)
=sin2x+cos2x=2sin(2x+).
|
x |
- |
|
|
|
|
|
ωx+φ |
0 |
|
π |
π |
2π |
|
f(x) |
0 |
2 |
0 |
-2 |
0 |
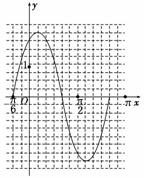 图.
图.
(2)由2kπ+≤2x+≤2kπ+(k∈Z)得
kπ+≤x≤kπ+(k∈Z),
故函数f(x)的单调减区间为[kπ+,kπ+](k∈Z).
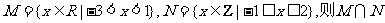 = ( )
= ( )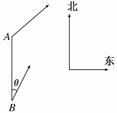 (本小题满分12分)如图所示,甲船由A岛出发向北偏东
(本小题满分12分)如图所示,甲船由A岛出发向北偏东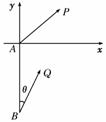 为10海里/小时.
为10海里/小时.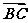
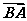 ·
·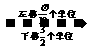 y=sin2x的图象.
y=sin2x的图象.