2.气体的体积、压强和温度的关系:对一定质量的理想气体(实际气体在常温下可视为理
想气体) (恒量)。
(恒量)。
[例题解析]
题型一 热现象和概念辨析
题型特点:题目一般选教材中一些重要的演示实验、常见热现象、重要概念的理解写成
选项,考查对重要热现象和热学概念的掌握情况。
解题策略:这类题目较基础,属于送分题。在平常的学习中,要关注对物理概念辨析的
有关说法(或否定)特例进行积累,正确理解基本概念、基本定律的形成过程。
例1.下列叙述正确的是 ( )
A.理想气体压强越大,分子的平均动能越大
B.自然界中进行的涉及热现象的宏观过程都具有方向性
C.外界对理想气体做正功,气体的内能不一定增大
D.温度升高,物体内每个分子的热运动速率都增大
解析:气体的压强是大量分子对器壁碰撞产生的,影响气体压强的因素有两个:分子的平均动能和气体分子密度,故A错;自发的热现象都具有方向性,所以B正确;改变物体的内能有两种方式,若对气体做正功的同时放出热量,则内能有可能减小,所以C也正确;单个分子的热运动具有无规则性和随机性,所以D选项错误,正确选项为BC。
点拨:该题重点是对有关热现象进行辨析,虽然是对多个现象进行了组合,但题目都比较简单,完全来源于教材。因此,在学习中要做到理解、识记基本的现象和一些特例,善于比较、鉴别一些似是而非的说法。
变式训练1:下列说法中正确的是 ( )
A.理想气体的压强是由于其受重力作用而产生的
B.热力学第二定律使人们认识到,自然界中进行的涉及热现象的宏观过程都具有方向
性
C.热力学温度的零度是一切物体低温的极限,只能无限接近,但不可能达到
D.气体分子的热运动的速率是遵循统计规律的 (答案:BD)
题型二 微观量的估算
题型特点:题目一般要以阿伏加德罗常数为联系桥梁对分子、原子或原子核进行有关量
的计算,考查对分子数量、分子大小的理解情况。
解题策略:这类题目较难度不是太大,但往往比较繁杂。在平常的学习中,要关注运算
能力的培养,要过细完成具体的运算过程。
例2. 粒子与金原子核发生对心碰撞时,能够接近金原子核中心的最小距离为
粒子与金原子核发生对心碰撞时,能够接近金原子核中心的最小距离为 m,
m,
已知金原子的摩尔质量为 kg/mol,阿伏加德罗常数为
kg/mol,阿伏加德罗常数为 个/mol,则
个/mol,则
由此可估算出金原子核的平均密度为 ( )
A. B.
B.
C. D.
D.
解析:lmol的任何物质,都含有NA(阿伏加德罗常数)个分子(或原子),其摩尔质量Mmol
恒等于NA个分子(或原子)质量为m的质量总和,据此可求出一个分子(或原子)的质量为
|
 。
。
把上述思路用于本题,一个金原子的质量为

金原子核几乎集中了金原子的全部质量,故可认为金原子核的质量 近似等于金原子
近似等于金原子
的质量m,如果把金原子核想象成一个球体,由 粒子能够接近金原子核中心的最小距
粒子能够接近金原子核中心的最小距
离可推知,金原子核的半径r近似等于且不会大于这一最小距离,综合上述两点,便可
求出金原子核的平均密度 近似等于且不会小于下式所求的值.即
近似等于且不会小于下式所求的值.即
 ,故选项B正确。
,故选项B正确。
点拨:估算固体或液体个分子(或原子)的直径和质量,要理解如下两个要点:
①忽略分子的间隙,建立理想化的微观结构模型,这是估算个分子(或原子)的体积和直
径数量级的基础。
②用阿伏加德罗常数NA把宏现量摩尔质量Mmol,与摩尔体积Vmol跟微观量分子质量m
与分子体积V联系起来。
变式训练2:假如全世界60亿人同时数1 g水的分子个数,每人每小时可以数5000个,
不间断地数,则完成任务所需时间最接近(阿伏加德罗常数NA取6×1023 mol-1)( )
A.10年 B.1千年 C.10万年 D.1千万年
(答案:C)
题型三 热学概念与规律的理解
题型特点:该类试题重点考查对热学基本概念与基本规律的理解,题目叙述简单但各个
选项迷惑性强,似是而非。
解题策略:正确解决热学问题的首要要求是清楚基本概念和基本规律, 概念重在理解,
一定要清楚它是从什么现象引出的,要注意各个基本概念之间常常存在因果关系,只有
善于把握这种因果关系才能抓住解决问题的关键。
例3.对一定量的气体,下列说法正确的是 ( )
A.在体积缓慢地不断增大的过程中,气体一定对外界做功
B.在压强不断增大的过程中,外界对气体一定做功
C.在体积不断增大的过程中,内能一定增加
D.在与外界没有发生热量交换的过程中,内能一定不变
解析:只要气体体积膨胀,气体就一定会对外界做功。故选项A正确;气体压强在不断
增大的过程中,外界不一定对气体做功,因为有可能是气体体积不变,从外界吸热,自
身温度升高,压强增大的情况,故选项B错误;气体体积在不断被压缩的过程中,外界
对气体做了功,但其内能不一定增加,因为有可能对外放出了热量,如果放出的热量大
于外界对气体做的功,其自身内能还要降低,故选项C错误;当气体在与外界没有发生
任何热量交换的过程中内能有可能要改变,因为改变内能有两种方式:做功和热传递,
故选项D错误。
点拨:根据能量守恒定律、热力学第一定律来分析问题,先要弄清楚能量的转化关系和
转化的方向,即物体是吸热还是放热,是物体对外做功还是外界对物体做功,最后判断
内能是增加还是减少。
变式训练3:地面附近有一正在上升的空气团,它与外界的热交热忽略不计.已知大气压
强随高度增加而降低,则该气团在此上升过程中(不计气团内分子间的势能)( )
A.体积减小,温度降低 B.体积减小,温度不变
C.体积增大,温度降低 D.体积增大,温度不变
(答案:C)
题型四 气体压强与气缸的应用
题型特点:气缸活塞类试题是考查气体压强问题的极好载体,对近几年各类考试题(尤
其是高考)进行研究,可以发现气缸活塞类问题是高考中的“常客”,该类试题重点考查
对热学基本规律的综合应用。
解题策略:一是要能够利用物体平衡条件求气体压强。对于求用固体(如活塞等)封闭
在静止容器内的气体压强问题,应对固体(如活塞等)进行受力分析,然后根据平衡条
件求解。二是要会用理想气体状态参量的关系分析问题。
例4.如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,
活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于容器的底部,另一端固
定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时
的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静
 止,气体达到平衡态,经过此过程 ( )
止,气体达到平衡态,经过此过程 ( )
A.EP全部转换为气体的内能
B.EP一部分转换成活塞的重力势能,其余部分仍为弹簧的弹性势能
C.EP全部转换成活塞的重力势能和气体的内能
D.EP一部分转换成活塞的重力势能,一部分转换为气体的内能,其
余部分仍为弹簧的弹性势能
解析:以活塞为研究对象,设初态时气体压强为P1,活塞质量为m,截面积为S,末态
时的压强为P2,初态: ,由题意可得末态位置必须高于初态位置,否则
,由题意可得末态位置必须高于初态位置,否则
|
 和
和 (绝热),W为正,
(绝热),W为正, 也必为正,温度升高,内能
也必为正,温度升高,内能
增加,活塞重力势能增加,末态时,由力的平衡条件知: ,仍然具有一
,仍然具有一
定弹性势能,D正确。
点拨:本题考查力学与气体、与热力学第一定律的综合应用,解答本题的关键是中间过
程不考虑,只考虑初、末状态,热力学第一定律是研究内能、热量与功之间关系的,反
映了改变内能的方式既可以通过做功也可以通过热传递。
变式训练4:如图所示,绝热气缸直立于地面上,光滑绝热活塞封闭一定质量的气体并
静止在A位置,气体分子间的作用力忽略不计,现将一个
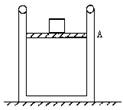 物体轻轻放在活塞上,活塞最终静止在B位置(图中未画
物体轻轻放在活塞上,活塞最终静止在B位置(图中未画
出),则活塞 ( )
A.在B位置时气体的温度与在A位置时气体的温度相同
B.在B位置时气体的压强比在A位置时气体的压强大
C.在B位置时气体单位体积内的分子数比在A位置时气
体单位体积内的分子数少
D.在B位置时气体分子的平均速率比在A位置时气体分子的平均速率大
(答案BD)
[专题训练与高考预测]
 为斥力,
为斥力,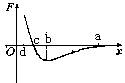 A.乙分子由a到b做加速运动,由b到c做减速运动
A.乙分子由a到b做加速运动,由b到c做减速运动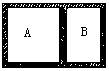 的体积,两部分温度相同,如图所示,若拔出销钉,达到平衡时,A、B两部分气体的体
的体积,两部分温度相同,如图所示,若拔出销钉,达到平衡时,A、B两部分气体的体