摘要：教师:下面请同学仔细观察屏幕中动画反映的事实.认真思考后“创新 一个题目.不用给出解答. (在教师即时制作动画时学生很容易直观地看出其意思.但对读者需作简单说明:点A.B是定点.圆D是一定圆.点C在圆D上运动.点G是△ABC两条中线的交点.即△ABC的重心.主动点C在定圆D上运动.从动点G随之运动) 同学们认真观察之后积极踊跃地写出了他们的“创新 题: 学生E:点A.B是定圆D外的两定点.点C在圆D上运动.点G是△ABC的重心.求动点G的轨迹方程. 学生F:点A.B是两定点.圆D是一定圆.点C在圆D上运动.动点G满足.求动点G的轨迹. 学生G:已知点.和圆.点C在圆D上运动.点G是△ABC三条中线的交点.求动点G的轨迹方程. 学生H:已知点.和圆.点C在圆D上运动.动点G满足.求动点G的轨迹. -------- 教师对每一位学生的“创新 给以肯定.对不同“创新 加以分析点评.
网址：http://m.1010jiajiao.com/timu_id_4450271[举报]
学习三角函数一章时，课堂上老师给出这样一个结论:当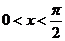
时，有
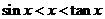恒成立，当老师把这个证明完成时，
(Ⅰ) 学生甲提出问题：能否在不等式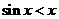
的左边增加一个量，使不等号的方向得以改变？
下面请同学们证明：若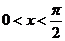，则
成立。
(Ⅱ) 当学生甲的问题完成时，学生乙提问：对于不等式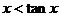
是否也有相似的结论？
下面请同学们探讨：若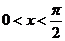，是否存在实数
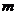，使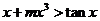
恒成立?如果存在,求出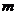的一个值;如果不存在,请说明理由.
查看习题详情和答案>>
学习三角函数一章时，课堂上老师给出这样一个结论:当
时，有
恒成立，当老师把这个证明完成时，
（Ⅰ） 学生甲提出问题：能否在不等式
的左边增加一个量，使不等号的方向得以改变？下面请同学们证明：若，则 
成立；
（Ⅱ） 当学生甲的问题完成时，学生乙提问：对于不等式
是否也有相似的结论？下面请同学们探讨：若，是否存在实数
，使
恒成立?如果存在,求出的一个值;如果不存在,请说明理由。
学习三角函数一章时，课堂上老师给出这样一个结论:当
时，有
恒成立，当老师把这个证明完成时，
(Ⅰ) 学生甲提出问题：能否在不等式
的左边增加一个量，使不等号的方向得以改变？
下面请同学们证明：若，则 
成立。
(Ⅱ) 当学生甲的问题完成时，学生乙提问：对于不等式
是否也有相似的结论？
下面请同学们探讨：若，是否存在实数
，使
恒成立?如果存在,求出的一个值;如果不存在,请说明理由.
时，有sinx＜x＜tanx恒成立，当老师把这个证明完成时，
成立；