题目内容
学习三角函数一章时,课堂上老师给出这样一个结论:当![]() 时,有
时,有![]() 恒成立,当老师把这个证明完成时,
恒成立,当老师把这个证明完成时,
(Ⅰ) 学生甲提出问题:能否在不等式![]() 的左边增加一个量,使不等号的方向得以改变?
的左边增加一个量,使不等号的方向得以改变?
下面请同学们证明:若![]() ,则
,则 ![]() 成立。
成立。
(Ⅱ) 当学生甲的问题完成时,学生乙提问:对于不等式![]() 是否也有相似的结论?
是否也有相似的结论?
下面请同学们探讨:若![]() ,是否存在实数
,是否存在实数![]() ,使
,使![]() 恒成立?如果存在,求出
恒成立?如果存在,求出![]() 的一个值;如果不存在,请说明理由.
的一个值;如果不存在,请说明理由.
解: (Ⅰ)证明:设![]() ,则
,则![]() ……………………………1
……………………………1
设![]() ,则
,则![]()
故当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
且曲线![]() 在
在![]() 处连续不断而
处连续不断而![]() ,……………………………5
,……………………………5
所以, 当![]() 时,
时, ![]() .
.
故当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
且曲线![]() 在
在![]() 处连续不断而
处连续不断而![]() ,
,
所以, 当![]() 时,
时, ![]() .即原不等式得证. ……………………………9
.即原不等式得证. ……………………………9
(Ⅱ)不存在.解析如下:
设![]() ,
,
① 若![]() ,由结论可知,
,由结论可知, ![]() ;……………………………10
;……………………………10
② 若![]() ,当
,当![]() 趋近于
趋近于![]() 时,
时,![]() 接近于某一个常数,而
接近于某一个常数,而![]() 趋近于
趋近于![]() ,不可能
,不可能
使![]() 恒成立.
恒成立.
综上所述, 不存在实数![]() 使
使![]() 恒成立. ……………………………12
恒成立. ……………………………12

练习册系列答案
相关题目
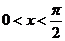 时,有
时,有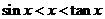 恒成立,当老师把这个证明完成时,
恒成立,当老师把这个证明完成时, 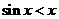 的左边增加一个量,使不等号的方向得以改变?
的左边增加一个量,使不等号的方向得以改变? 成立。
成立。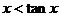 是否也有相似的结论?
是否也有相似的结论?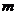 ,使
,使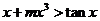 恒成立?如果存在,求出
恒成立?如果存在,求出