摘要:26.(1)解:由得点坐标为 由得点坐标为 ∴··················································································· 由解得∴点的坐标为···································· ∴··························································· (2)解:∵点在上且 ∴点坐标为······················································································ 又∵点在上且 ∴点坐标为······················································································ ∴··········································································· (3)解法一:当时.如图1.矩形与重叠部分为五边形(时.为四边形).过作于.则 ∴即∴ ∴ 即··································································· 29. 问题解决 如图(1).将正方形纸片折叠.使点落在边上一点(不与点.重合).压平后得到折痕.当时.求的值. 类比归纳 在图(1)中.若则的值等于 ,若则的值等于 ,若(为整数).则的值等于 .(用含的式子表示) 联系拓广 如图(2).将矩形纸片折叠.使点落在边上一点(不与点重合).压平后得到折痕设则的值等于 .(用含的式子表示)
网址:http://m.1010jiajiao.com/timu_id_4444538[举报]
解:(1)OA=1,OC=2
则A点坐标为(0,1),C点坐标为(2,0)
设直线AC的解析式为y=kx+b
![]()
解得
![]() 直线AC的解析式为
直线AC的解析式为![]() ··················· 2分
··················· 2分
(2)![]() 或
或![]()
(正确一个得2分)························· 8分
 (3)如图,设
(3)如图,设![]()
过![]() 点作
点作![]() 于F
于F
![]()
由折叠知![]()
![]()
![]() 或2··········· 10分
或2··········· 10分
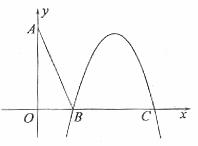
在直角坐标系xOy中,设点A(0,t),点Q(t,b)(t,b均为非零常数).平移二次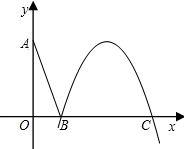 函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.
函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.
(1)是否存在这样的抛物线F,使得|OA|2=|OB|•|OC|?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=
,求抛物线F对应的二次函数的解析式.
查看习题详情和答案>>
 函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.
函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.(1)是否存在这样的抛物线F,使得|OA|2=|OB|•|OC|?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=
| 3 | 2 |
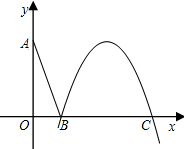 函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.
函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB. ,求抛物线F对应的二次函数的解析式.
,求抛物线F对应的二次函数的解析式.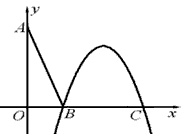
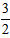 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。