题目内容

解：（1）OA=1，OC=2

则A点坐标为（0，1），C点坐标为（2，0）

设直线AC的解析式为y=kx+b

解得

直线AC的解析式为··················· 2分

（2）或

（正确一个得2分）························· 8分

（3）如图，设

过点作于F

由折叠知

或2··········· 10分

如图，在平面直角坐标系中，点关于轴的对称点为，与轴交于点，将△沿翻折后，点落在点处．

（1）求点、的坐标；

（2）求经过、、三点的抛物线的解析式；

（3）若抛物线的对称轴与交于点，点为线段上一点，过点作轴的平行线，交抛物线于点．

①当四边形为等腰梯形时，求出点的坐标；

②当四边形为平行四边形时，直接写出点的坐标.

练习册系列答案
相关题目
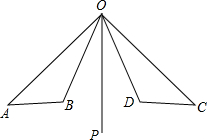精英家教网已知：如图，OP是∠AOC和∠BOD的平分线，OA=OC，OB=OD．
试说明：AB=CD．
解：∵OP是∠AOC和∠BOD的平分线
∴∠AOP=
 
，∠BOP=
 
，
∴∠AOP-∠BOP=∠COP-∠DOP
即∠
 
=∠
 

在△ABO和△CDO中
OA=OC
(--------)
OB=OD
，
∴
 
≌
 
   （
 
）
∴
 
=
 
   （全等三角形的对应边相等）
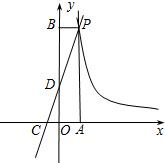精英家教网如图，一次函数y=kx+2的图象与反比例函数y=
m
x
的图象在第一象限交于点P，PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交x、y轴于点C、D，S△PBD=4，CO：OA=1：2．
（1）求点D的坐标；
（2）求一次函数与反比例函数的解析式；
（3）当x＞0时，不等式kx+2＞
m
x
的解集是
 
．
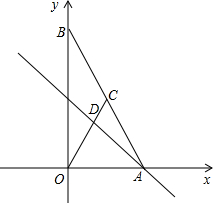如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长（0A＜OB）是方程组
2x=y
3x-y=6
的解，点C是直线y=2x与直线AB的交点，点D在线段OC上，OD=2
5
．
（1）求直线AB的解析式及点C的坐标；
（2）求直线AD的解析式；
（3）P是直线AD上的点，在平面内是否存在点Q，使以0、A、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
如图，在平面直角坐标系中，直线AB：y=kx+b与直线OA：y=mx相交于点A（-1，-2），则关于x的不等式kx+b＜mx的解是
x＞-1
x＞-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网