摘要：17． 杨辉三角是杨辉的一大重要研究成果.它的许多性质与组合数的性质有关.杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角: (1)求第20行中从左到右的第4个数,(2)若第n行中从左到右第14与第15个数的比为.求n的值,杨辉三角的所有数的和, (4)在第3斜列中.前5个数依次为1.3.6.10.15,第4斜列中.第5个数为35.显然.1+3+6+10+15=35.事实上.一般地有这样的结论: 第m斜列中前k个数之和.一定等于第m+1斜列中第k个数. 试用含有m.k的数学公式表示上述结论.并给予证明.
网址：http://m.1010jiajiao.com/timu_id_4443255[举报]
杨辉是我国南宋著名的数学家，“杨辉三角”是杨辉的一大重要研究成果，其中蕴含了许多优美的规律（如图），“杨辉三角”中第14行从左到右第10与第11个数的比值为杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图所示是一个11阶杨辉三角：
（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为
，求n的值；
（3）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m，k（m，k∈N*）的数学公式表示上述结论，并给予证明．
查看习题详情和答案>>
（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为
| 2 | 3 |
（3）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m，k（m，k∈N*）的数学公式表示上述结论，并给予证明．
杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共5种21卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下图是一个11阶的杨辉三角:
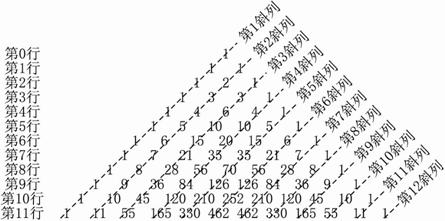
试回答:(其中第(1)&(5)小题只需直接给出最后的结果,无需求解过程)
(1)记第i(i∈N*)行中从左到右的第j(j∈N*)个数为aij,则数列{aij}的通项公式为 ,
n阶杨辉三角中共有 个数;
(2)第k行各数的和是;
(3)n阶杨辉三角的所有数的和是;
(4)将第n行的所有数按从左到右的顺序合并在一起得到的多位数等于;
(5)第p(p∈N*,且p≥2)行除去两端的数字1以外的所有数都能被p整除,则整数p一定为( )
A.奇数 B.质数 C.非偶数 D.合数
(6)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k(m、k∈N*)的数学公式表示上述结论并证明其正确性.
数学公式为 .
证明: .
查看习题详情和答案>>
，求n的值；
的数学公式表示上述结论，并给予证明. 
，求n的值；
的数学公式表示上述结论，并给予证明. 