摘要:[选做题]在A.B.C.D四小题中只能选做两题.每小题10分.共计20分.请在答题卡指定区域内作答.解答时应写出文字说明.证明过程或演算步骤. A.选修4 - 1:几何证明选讲 如图.在四边形ABCD中.△ABC≌△BAD. 求证:AB∥CD. [解析] 本小题主要考查四边形.全等三角形的有关知识.考查推理论证能力.满分10分. 证明:由△ABC≌△BAD得∠ACB=∠BDA.故A.B.C.D四点共圆.从而∠CBA=∠CDB.再由△ABC≌△BAD得∠CAB=∠DBA.因此∠DBA=∠CDB.所以AB∥CD. B. 选修4 - 2:矩阵与变换 求矩阵的逆矩阵. [解析] 本小题主要考查逆矩阵的求法.考查运算求解能力.满分10分. 解:设矩阵A的逆矩阵为则 即故 解得:. 从而A的逆矩阵为. C. 选修4 - 4:坐标系与参数方程 已知曲线C的参数方程为(为参数.). 求曲线C的普通方程. [解析] 本小题主要考查参数方程和普通方程的基本知识.考查转化问题的能力.满分10分. 解:因为所以 故曲线C的普通方程为:. D. 选修4 - 5:不等式选讲 设≥>0,求证:≥. [解析] 本小题主要考查比较法证明不等式的常见方法.考查代数式的变形能力.满分10分. 证明: 因为≥>0,所以≥0.>0.从而≥0. 即≥. 2009海南宁夏卷 选修4-1,几何证明选讲 如图.已知ABC中的两条角平分线和相交于.B=60.在上.且. (1)证明:四点共圆, (2)证明:CE平分DEF. (22)解: (Ⅰ)在△ABC中.因为∠B=60°. 所以∠BAC+∠BCA=120°. 因为AD,CE是角平分线. 所以∠HAC+∠HCA=60°. 故∠AHC=120°. 于是∠EHD=∠AHC=120°. 因为∠EBD+∠EHD=180°. 所以B,D,H,E四点共圆. (Ⅱ)连结BH.则BH为的平分线.得30° 由(Ⅰ)知B.D.H.E四点共圆. 所以30° 又60°.由已知可得. 可得30° 所以CE平分 选修4-4:坐标系与参数方程. 已知曲线C: . C:(为参数). (1)化C.C的方程为普通方程.并说明它们分别表示什么曲线, (2)若C上的点P对应的参数为.Q为C上的动点.求中点到直线 距离的最小值. (23)解: (Ⅰ) 为圆心是.半径是1的圆. 为中心是坐标原点.焦点在轴上.长半轴长是8.短半轴长是3的椭圆. (Ⅱ)当时..故 为直线. M到的距离 从而当时.取得最小值 选修4-5:不等式选讲 如图.为数轴的原点.为数轴上三点.为线段上的动点.设表示与原点的距离. 表示到距离4倍与到距离的6倍的和. (1)将表示为的函数, (2)要使的值不超过70. 应该在什么范围内取值? (24)解: (Ⅰ) (Ⅱ)依题意.满足 解不等式组.其解集为 所以 2009辽宁理卷 选修 4- l :几何证明选讲 己知△ABC中.AB=AC , D是△ABC外接圆 劣弧上的点.延长BD至E. (1)求证:AD 的延长线平分, (2)若.△ABC中BC边上的高, 求△ABC外接圆的面积. 如图.设F为AD延长线上一点.∵A.B.C. D 四点共圆. = . 又AB=AC .∴.且. ∴.对顶角.故. 故AD 的延长线平分. .( 2)设O为外接圆圆心.连接AO交BC于H .则AH⊥BC , 连接 OC .由题意OAC=OCA =.. ∴.设圆半径为r.则. 得:r= 2 .故外接圆面积为. 选修 4- 4 :极坐标与参数方程 在直角坐标系xOy中.以O为极点.x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为.M , N分别为曲线C与x轴.y轴的交点. (1)写出曲线C的直角坐标方程.并求M , N的极坐标, (2)设M , N的中点为P.求直线OP的极坐标方程. 由得:. ∴曲线C的直角坐标方程为.即. 当时..∴M的极坐标(2.0), 当时..∴N的极坐标. .N的直角坐标为.∴P的直角坐标为. 则P的极坐标为.直线OP的极坐标方程为.----10分 选修 4- 5 :不等式选讲 设函数. (1)若.解不等式, (2)如果..求a的取值范围. 当时..由得:. 由绝对值的几何意义知不等式的解集为. 不等式可化为或或. ∴不等式的解集为. (2)若..不满足题设条件, 若..的最小值为, 若..的最小值为. 所以对于.的充要条件是.从而a的取值范围.
网址:http://m.1010jiajiao.com/timu_id_4441076[举报]
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.A选修4-1:几何证明选讲
如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.
求证:∠ACB=
| 1 |
| 3 |
B选修4-2:矩阵与变换
已知矩阵A=
|
| β |
|
| a |
| a |
| β |
C选修4-3:坐标系与参数方程
已知椭圆C的极坐标方程为ρ2=
| a |
| 3cos2θ+4sin2θ |
D选修4-4:不等式选讲
已知函数f(x)=(x-a)2+(x-b)2+(x-c)2+
| (a+b+c)2 |
| 3 |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,求线段AE的长.
B.(选修4-2:矩阵与变换)
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
|
|
C.(选修4-4:坐标系与参数方程)
以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,建立极坐标系(两种坐标系中取相同的单位长度),已知点A的直角坐标为(-2,6),点B的极坐标为(4,
| π |
| 2 |
| π |
| 4 |
D.(选修4-5:不等式选讲)
设a,b,c,d都是正数,且x=
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵
|
C.(选修4-4:坐标系与参数方程)
已知曲线C1:
|
| π |
| 4 |
| 2 |
(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<
| c |
| 4 |
| c |
| 6 |
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
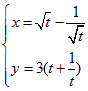 (
(