摘要:1建筑工地上一堆圆木.从上到下每层的数目分别为1.2.3.--.10 . 问共有多少根圆木?如何用简便的方法 三探究发现 变式: 问题1若把问题变成求:1+2+3+4+‥ ‥ +99=?可以用哪些方法求出来呢? 方法1:原式=(1+2+3+4+‥ ‥ +99+100)-100 方法2:原式=+99 方法3:原式=0+1+2+3+4+‥ ‥ +98+99 方法4:原式=(1+2+3+4+‥ +49+51+52+‥ 99)+50 方法5:原式=(1+2+3+4+‥ ‥ +98+99+99+98+‥ +2+1)÷ 2 方法6 令 S=1+2+3+4+‥ ‥ +99 又 S=99+98+97+‥ +2+1 故 2S=+‥ ‥ + 从而 S =÷ 2 = 4950 问题2:1+2+3+4+‥ ‥ +(n-1)+n=? 在上面6种方法中.哪个能较好地推广应用于这个式子的求和? 令 Sn =1+2+3+4+‥ ‥ +n. 则 Sn =n+(n-1)+‥ ‥ +2+1 从而有 2Sn = + =(n+1)n 上述求解过程带给我们什么启示? (1)所求的和可以用首项.末项及项数来表示, (2)等差数列中任意的第k项与倒数第k项的和都等于首项与末项的和. 问题 3:现在把问题推广到更一般的情形: 设数列 {an }为等差数列.它的首项为a1 . 公差为d. 试求 Sn =a1 +a2 + a3 +‥ ‥ + an-1 +an (I) an=a1+得 Sn=na1+ d(II) 等差数列{an}的首项为a1.公差为d.项数为n.第n项为an.前n项和为Sn.请填写下表: a1 d n an sn 5 10 10 -2 50 2550 -38 -10 -360 14.5 26 32 说明:两个等差数列的求和公式及通项公式.一共涉及到5个量.通常已知其中3个.可求另外2个.
网址:http://m.1010jiajiao.com/timu_id_4440133[举报]
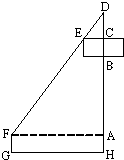 如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)
如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)(Ⅰ)记工件能被吊起的最大高度为y(m),请选取适当的变量将y表示成该变量的函数;
(Ⅱ)判断工件能否安全被吊到桥墩上,并说明理由.(参考数据:
| 3 |
如下图,建筑工地有一用细砂堆成的多面体,其上下两个底面平行且都是矩形,上底面矩形的两边分别为6 m与3 m,下底面矩形的长边为10 m,若此多面体的四个侧面与底面所成的二面角都相等,则其下底面的短边边长为( )

A.7m B.6m C.5m D.4 m
查看习题详情和答案>>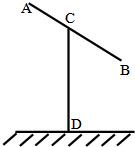 某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.
某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.(1)设AB=2x,CD=y,试用x表示y;
(2)怎样设计AB、CD的长,可使建造这个支架的成本最低? 查看习题详情和答案>>
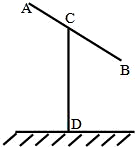 某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.
某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.