题目内容
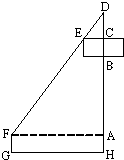 如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)
如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)(Ⅰ)记工件能被吊起的最大高度为y(m),请选取适当的变量将y表示成该变量的函数;
(Ⅱ)判断工件能否安全被吊到桥墩上,并说明理由.(参考数据:
| 3 |
分析:(I)取吊臂的张角∠AFD=θ为变量,由图可知,y=AB+1.1=AD-BC-CD+1.1=DFsiθ-2-CEtanθ+1.1=24sinθ-3tanθ-0.9=24sinθ-3tanθ-0.9(0<θ<
)
(Ⅱ)利用导数求出y的最大值,与15比较,作出判断.
| π |
| 2 |
(Ⅱ)利用导数求出y的最大值,与15比较,作出判断.
解答:解:(I)取吊臂的张角∠AFD=θ为变量,吊车能把工件吊起的最大高度y取决于θ.
由图可知,y=AB+1.1=AD-BC-CD+1.1=DFsiθ-2-CEtanθ+1.1=24sinθ-3tanθ-0.9(0<θ<
).…(4分)
(II)吊车不能把圆柱形工件吊起平放到15m高的桥墩上.…(5分)
由(I)知,y′=24cosθ-
.
令,y′=0,解得cosθ=
,∴θ=
.…(8分)
当θ∈(0,
)时,
<cosθ<1,此时,y′=24cosθ-
=
>0;
当θ∈(
,
)时,0<cosθ<
,此时y′=24cosθ-
=
<0;.
故当,∴θ=
时,y有最大值,且最大值为y=9
-0.9=14.688<15.…(11分)
∴吊车不能把圆柱形工件吊起平放到15m高的桥墩上.…(12分)
由图可知,y=AB+1.1=AD-BC-CD+1.1=DFsiθ-2-CEtanθ+1.1=24sinθ-3tanθ-0.9(0<θ<
| π |
| 2 |
(II)吊车不能把圆柱形工件吊起平放到15m高的桥墩上.…(5分)
由(I)知,y′=24cosθ-
| 3 |
| cos2θ |
令,y′=0,解得cosθ=
| 1 |
| 2 |
| π |
| 3 |
当θ∈(0,
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| cos2θ |
| 24cos3θ-3 |
| cos2θ |
当θ∈(
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| 3 |
| cos2θ |
| 24cos3θ-3 |
| cos2θ |
故当,∴θ=
| π |
| 3 |
| 3 |
∴吊车不能把圆柱形工件吊起平放到15m高的桥墩上.…(12分)
点评:本题主要考查解三角形的实际应用.当涉及最值问题时,可借助函数的单调性来解决.

练习册系列答案
相关题目
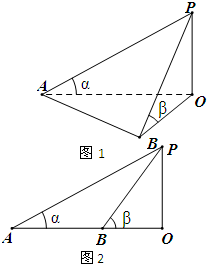 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.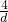 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大? ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?