摘要:解:如图5-22.建立空间直角坐标系O-xyz. (1)依题意得B.N ∴| |=. (2)依题意得A1.B.C.B1 ∴={-1.-1.2}.={0.1.2.}.·=3.||=.||= ∴cos<.>=. (3)证明:依题意.得C1.M(.2).={-1.1.2}. ={.0}. ∴·=-+0=0.∴⊥.∴A1B⊥C1M. 评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件.
网址:http://m.1010jiajiao.com/timu_id_4435244[举报]
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.

(Ⅰ)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(Ⅱ)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为S=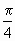 lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
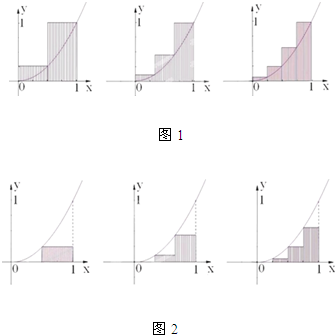 为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.
为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.(1)求a2,a3,a4;
(2)求an的通项公式,并证明an>
| 1 |
| 3 |
(3)求bn的通项公式,类比第②步,猜想bn的取值范围.并由此推出S的值(只需直接写出bn的范围与S的值,无须证明).
参考公式:12+22+32+…+(n-1)2+n2=
| 1 |
| 6 |
(本题满分15分)如图,某机场建在一个海湾的半岛上,飞机跑道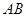 的长为4.5
的长为4.5 ,且跑道所在的直线与海岸线
,且跑道所在的直线与海岸线 的夹角为
的夹角为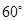 (海岸线可以看作是直线),跑道上离海岸线距离最近的点
(海岸线可以看作是直线),跑道上离海岸线距离最近的点 到海岸线的距离
到海岸线的距离 .
.
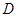 为海湾一侧海岸线
为海湾一侧海岸线 上的一点,设
上的一点,设 ,点
,点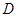 对跑道
对跑道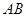 的视角为
的视角为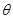 .
.
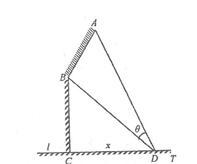
(1)
将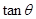 表示为
表示为 的函数;
的函数;
(2)已知常数 ,对于任意的
,对于任意的 ,
,
 ,等号成立当
,等号成立当
且仅当 ,求点
,求点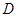 相对于垂足
相对于垂足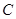 的位置,使
的位置,使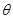 取得最大值.
取得最大值.
查看习题详情和答案>>

