摘要：19．(1) 设函数.且数列满足= 1.(n∈N.),求数列的通项公式． (2)设等差数列.的前n项和分别为和.且 .. ,求常数A的值及的通项公式． (3)若.其中.即为中的数列.的第项.试求．
网址：http://m.1010jiajiao.com/timu_id_4430437[举报]
（1）设函数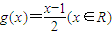
，且数列{cn}满足c1=1，cn=g（cn-1）（n∈N，n＞1）；求数列{cn}的通项公式．
（2）设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且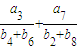
=
，
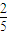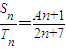，S2=6；求常数A的值及{an}的通项公式．
（3）若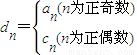
，其中an、cn即为（1）、（2）中的数列{an}、{cn}的第n项，试求d1+d2+…+dn．
查看习题详情和答案>>
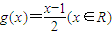，且数列{cn}满足c1=1，cn=g（cn-1）（n∈N，n＞1）；求数列{cn}的通项公式．（2）设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且
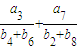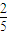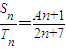=，，S2=6；求常数A的值及{an}的通项公式．（3）若
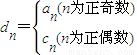，其中an、cn即为（1）、（2）中的数列{an}、{cn}的第n项，试求d1+d2+…+dn．查看习题详情和答案>>
（1）设函数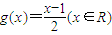
，且数列{cn}满足c1=1，cn=g（cn-1）（n∈N，n＞1）；求数列{cn}的通项公式．
（2）设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且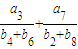
=
，
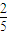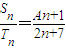，S2=6；求常数A的值及{an}的通项公式．
（3）若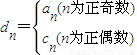
，其中an、cn即为（1）、（2）中的数列{an}、{cn}的第n项，试求d1+d2+…+dn．
查看习题详情和答案>>
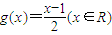，且数列{cn}满足c1=1，cn=g（cn-1）（n∈N，n＞1）；求数列{cn}的通项公式．（2）设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且
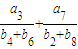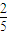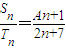=，，S2=6；求常数A的值及{an}的通项公式．（3）若
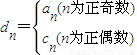，其中an、cn即为（1）、（2）中的数列{an}、{cn}的第n项，试求d1+d2+…+dn．查看习题详情和答案>>
设函数f(x)=
(a＞0)为奇函数，且|f(x)|min=2
，数列{an}与{bn}满足如下关系：a1=2，an+1=
，bn=
.
（1）求f（x）的解析式；
（2）求数列{bn}的通项公式bn；
（3）记Sn为数列{an}的前n项和，求证：对任意的n∈N*有Sn＜n+
.
查看习题详情和答案>>
| ax2+bx+1 |
| x+c |
| 2 |
| f(an)-an |
| 2 |
| an-1 |
| an+1 |
（1）求f（x）的解析式；
（2）求数列{bn}的通项公式bn；
（3）记Sn为数列{an}的前n项和，求证：对任意的n∈N*有Sn＜n+
| 3 |
| 2 |