摘要:解:(1)过C:上一点作斜率为的直线交C于另一点. 则. ----------------------------3分 于是有: 即: ----------------------------4分 (2)记.则 . ----------------6分 因为. 因此数列{}是等比数列. ----------------------------8分 可知:. . ----------------------------9分 当n为偶数时有: =. -----------------11分 于是 ①在n为偶数时有: . -----------------12分 ②在n为奇数时.前n-1项为偶数项.于是有: . -----------------13分 综合①②可知原不等式得证. ----------------------------14分
网址:http://m.1010jiajiao.com/timu_id_4398058[举报]
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
查看习题详情和答案>>
已知 、
、 ,椭圆C的方程为
,椭圆C的方程为 ,
, 、
、 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设 为椭圆C上一点,存在以
为椭圆C上一点,存在以 为圆心的
为圆心的 与
与 外切、与
外切、与 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作斜率为
作斜率为 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与 轴相交于点D,若
轴相交于点D,若
 求
求 的值;
的值;
(Ⅲ)已知真命题:“如果点T( )在椭圆
)在椭圆 上,那么过点T
上,那么过点T
的椭圆的切线方程为 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
查看习题详情和答案>>
(理)设斜率为k1的直线L交椭圆C:
+y2=1于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
+
=1
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
-
=1(a>0,b>0)中相类似的结论,并证明你的结论.
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
| x2 |
| 2 |
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
(本小题满分13分)已知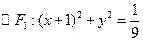 、
、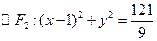 ,椭圆C的方程为
,椭圆C的方程为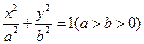 ,
,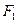 、
、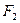 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设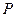 为椭圆C上一点,存在以
为椭圆C上一点,存在以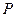 为圆心的
为圆心的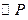 与
与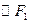 外切、与
外切、与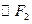 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点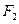 作斜率为
作斜率为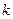 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与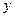 轴相交于点D,若
轴相交于点D,若
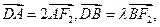 求
求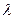 的值;
的值;
(Ⅲ)已知真命题:“如果点T(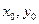 )在椭圆
)在椭圆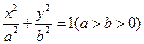 上,那么过点T
上,那么过点T
的椭圆的切线方程为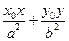 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线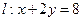 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
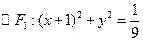 、
、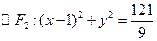 ,椭圆C的方程为
,椭圆C的方程为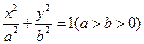 ,
,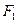 、
、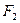 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设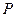 为椭圆C上一点,存在以
为椭圆C上一点,存在以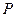 为圆心的
为圆心的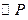 与
与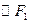 外切、与
外切、与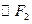 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
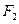 作斜率为
作斜率为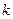 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与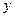 轴相交于点D,若
轴相交于点D,若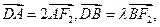 求
求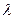 的值;
的值;(Ⅲ)已知真命题:“如果点T(
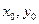 )在椭圆
)在椭圆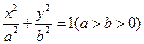 上,那么过点T
上,那么过点T的椭圆的切线方程为
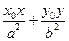 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:已知点Q是直线
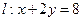 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
(2007•杨浦区二模)(理)设斜率为k1的直线L交椭圆C:
+y2=1于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
+
=1
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
-
=1(a>0,b>0)中相类似的结论,并证明你的结论.
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.
查看习题详情和答案>>
| x2 |
| 2 |
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
(3)分析(2)中的探究结果,并作出进一步概括,使上述结果都是你所概括命题的特例.
如果概括后的命题中的直线L过原点,P为概括后命题中曲线上一动点,借助直线L及动点P,请你提出一个有意义的数学问题,并予以解决.