题目内容
在直角坐标系 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 ,直线
,直线 与轨迹C交于A,B两点.
与轨迹C交于A,B两点.
(Ⅰ)写出轨迹C的方程; (Ⅱ)若

 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有| |>|
|>| |
|
【答案】
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴 ,故曲线C的方程为
,故曲线C的方程为 .
………………4分
.
………………4分
(Ⅱ)设 ,其坐标满足
,其坐标满足
消去y并整理得 ,故
,故 .
.
若 ,即
,即 .而
.而 ,
,
于是 ,化简得
,化简得 ,所以
,所以 .
.
(Ⅲ)


 .因为A在第一象限,故
.因为A在第一象限,故 .由
.由 知
知 ,从而
,从而 .又
.又 ,故
,故 ,即在题设条件下,恒有
,即在题设条件下,恒有 .
.
【解析】略

练习册系列答案
相关题目
 中,点p到两点
中,点p到两点 的距离之和等于4,
的距离之和等于4, 与C交于A、B两点,
与C交于A、B两点,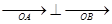 ,求k的值。
,求k的值。 中,点P到两定点
中,点P到两定点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 ,过点
,过点