题目内容
在直角坐标系
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与C交于A，B两点．
（1）写出C的方程；
（2）若OA
OB，求k的值
（1）
（2）
解析:
（1）设P( x，y )，由椭圆定义可知，点P的轨迹C是以，为焦点，
长半轴为2的椭圆．它的短半轴
， ……………………… 3分
故曲线C的方程为． ………………………………………………… 5分
（2）设
，其坐标满足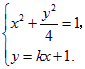
消去y并整理得
.
故
．………………………………………… 8分
若OAOB，即
．而
，
于是
，
化简，得
，所以．
因为△= 4k2+12(k2+4)=16k2+4>0对于任意的k∈R都成立.
故所求. ………………………………………………………………… 13分
练习册系列答案
相关题目
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与C交于A，B两点．
，求k的值；
中，点p到两点
的距离之和等于4，
与C交于A、B两点，
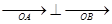，求k的值。
中，点P到两定点
，
的距离之和等于4，设点P的轨迹为
，过点
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与轨迹C交于A，B两点．
，求k的值；