摘要:3.重视对数学思想.方法进行归纳提炼.达到优化解题思维.简化解题过程 ①方程思想.解析几何的题目大部分都以方程形式给定直线和圆锥曲线.因此把直线与圆锥曲线相交的弦长问题利用韦达定理进行整体处理.就简化解题运算量. ②用好函数思想方法 对于圆锥曲线上一些动点.在变化过程中会引入一些相互联系.相互制约的量.从而使一些线的长度及a.b.c.e之间构成函数关系.函数思想在处理这类问题时就很有效. ③掌握坐标法 坐标法是解析几何的基本方法.因此要加强坐标法的训练. ④对称思想 由于圆锥曲线和圆都具有对称性质.可使分散的条件相对集中.减少一些变量和未知量.简化计算.提高解题速度.促成问题的解决. ⑤参数思想 参数思想是辩证思维在数学中的反映.一旦引入参数.用参数来划分运动变化状态.利用圆.椭圆.双曲线上点用参数方程形式设立或(x0.y0)即可将参量视为常量.以相对静止来控制变化.变与不变的转化.可在解题过程中将其消去.起到“设而不求 的效果. ⑥转化思想 解决圆锥曲线时充分注意直角坐标与极坐标之间有联系.直角坐标方程与参数方程.极坐标之间联系及转化.利用平移得出新系坐标与原坐标之间转化.可达到优化解题的目的. 除上述常用数学思想外.数形结合.分类讨论.整体思想.构造思想也是不可缺少的思想方法.复习也应给予足够的重视.
网址:http://m.1010jiajiao.com/timu_id_4393043[举报]
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
查看习题详情和答案>>
在高二年级某班学生在数学校本课程选课过程中,已知第一小组与第二小组各有六位同学.每位同学都只选了一个科目,第一小组选《数学运算》的有1人,选《数学解题思想与方法》的有5人,第二小组选《数学运算》的有2人,选《数学解题思想与方法》的有4人,现从第一、第二两小组各任选2人分析选课情况.
(Ⅰ)求选出的4人均选《数学解题思想与方法》的概率;
(Ⅱ)设ξ为选出的4个人中选《数学运算》的人数,求ξ的分布列和数学期望. 查看习题详情和答案>>
(Ⅰ)求选出的4人均选《数学解题思想与方法》的概率;
(Ⅱ)设ξ为选出的4个人中选《数学运算》的人数,求ξ的分布列和数学期望. 查看习题详情和答案>>
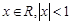 时,有如下表达式:
时,有如下表达式:  两边同时积分得:
两边同时积分得: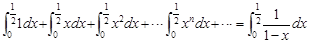


 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。