题目内容
(2013•福建)当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…=
两边同时积分得:
1dx+
xdx+
x2dx+…
xndx+…=
dx
从而得到如下等式:1×
+
×(
)2+
×(
)3+…+
×(
)n+1+…=ln2.
请根据以上材料所蕴含的数学思想方法,计算:
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
[(
)n+1-1].
| 1 |
| 1-x |
两边同时积分得:
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
从而得到如下等式:1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
请根据以上材料所蕴含的数学思想方法,计算:
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
分析:根据二项式定理得Cn0+Cn1x+Cn2x2+…+Cnnxn=(1+x)n,两边同时积分整理后,整理即可得到结论.
解答:解:二项式定理得Cn0+Cn1x+Cn2x2+…+Cnnxn=(1+x)n,
对Cn0+Cn1x+Cn2x2+…+Cnnxn=(1+x)n
两边同时积分得:
1
dx+
xdx+
x2dx+…+
xndx=
(1+x)ndx
从而得到如下等式:
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
故答案为:
[(
)n+1-1].
对Cn0+Cn1x+Cn2x2+…+Cnnxn=(1+x)n
两边同时积分得:
| ∫ |
0 |
| C | 0 n |
| ∫ |
0 |
| C | 1 n |
| ∫ |
0 |
| C | 2 n |
| ∫ |
0 |
| C | n n |
| ∫ |
0 |
从而得到如下等式:
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
故答案为:
| 1 |
| n+1 |
| 3 |
| 2 |
点评:本题主要考查二项式定理的应用.是道好题,解决问题的关键在于对Cn0+Cn1x+Cn2x2+…+Cnnxn=(1+x)n,两边同时积分,要是想不到这一点,就变成难题了.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
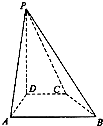 (2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.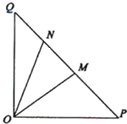 (2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
(2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2