摘要:(1)解:f(0)=f=0·f(0)+0·f(0)=0 由f(1)=f=1·f(1)+1·f(1). 得f(1)=0. (2)f(x)是奇函数 证明:因为f(1)=f[(-1)2]=-f(-1)-f(-1)=0 所以f(-1)=0 f(-x)=f(-1·x)=-f(x)+xf(-1)=-f(x). 因此.f(x)为奇函数 (3)证明:先用数学归纳法证明un=f(2n)>0(n∈N) ①当n=1时.u1=f(2)=2>0, ②假设当n=k时.uk=f(2k)>0 那么当n=k+1时.uk+1=f(2k+1)=2f(2k)+2kf(2)=2f(2k)+2k+1>0. 由以上两步可知.对任意n∈N.un=f(2n)>0. 因为un>0(n∈N) 所以un+1=f(2n+1)=2f(2n)+2nf(2)=2un+2n+1>un(n∈N)
网址:http://m.1010jiajiao.com/timu_id_4392393[举报]
设f(x)=
a>0且a≠1),g(x)是f(x)的反函数.
(Ⅰ)设关于x的方程求loga
=g(x)在区间[2,6]上有实数解,求t的取值范围;
(Ⅱ)当a=e,e为自然对数的底数)时,证明:
g(k)>
;
(Ⅲ)当0<a≤
时,试比较|
f(k)-n|与4的大小,并说明理由.
查看习题详情和答案>>
| 1+ax |
| 1-ax |
(Ⅰ)设关于x的方程求loga
| t |
| (x2-1)(7-x) |
(Ⅱ)当a=e,e为自然对数的底数)时,证明:
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
(Ⅲ)当0<a≤
| 1 |
| 2 |
| n |
 |
| k=1 |
设f(x)=|lgx|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足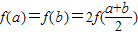 ,求证:①a•b=1;②
,求证:①a•b=1;②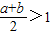 .
.
(3)在(2)的条件下,求证:由关系式 所得到的关于b的方程h(b)=0,存在b∈(3,4),使h(b)=0.
所得到的关于b的方程h(b)=0,存在b∈(3,4),使h(b)=0.
查看习题详情和答案>>
(1)求方程f(x)=1的解;
(2)若a,b满足
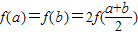 ,求证:①a•b=1;②
,求证:①a•b=1;②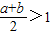 .
.(3)在(2)的条件下,求证:由关系式
 所得到的关于b的方程h(b)=0,存在b∈(3,4),使h(b)=0.
所得到的关于b的方程h(b)=0,存在b∈(3,4),使h(b)=0.查看习题详情和答案>>
如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),且其面积为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于A的一点,连接PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R.
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似?若存在,请找出M点的位置;若不存在,请说明理由.

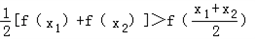 .
.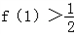 ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.