Question

设f（x）=|lgx|，a，b为实数，且0＜a＜b．
（1）求方程f（x）=1的解；
（2）若a，b满足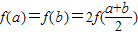，求证：①a•b=1；②．
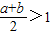（3）在（2）的条件下，求证：由关系式所得到的关于b的方程h（b）=0，存在b∈（3，4），使h（b）=0．

Answer 1

【答案】分析：（1）由f（x）=1得，lgx=±1，由此能求出方程f（x）=1的解．
（2）结合函数图象，由f（a）=f（b），知a∈（0，1），b∈（1，+∞），从而ab=-1．由=，构造函数能够证明．
（3）由b=（）²，得4b=a²+b²+2ab，令g（b）=，能推导出方程存在3＜b＜4的根．
解答：（1）解：由f（x）=1得，lgx=±1，
所以x=10，或x=．…（3分）
（2）证明：结合函数图象，由f（a）=f（b），
知a∈（0，1），b∈（1，+∞），…（4分）
从而-lga=lgb，从而ab=-1．…（5分）
又=，…（6分）
令．…（7分）
任取1＜b₁＜b₂，
∵∅（b₁）-∅（b₂）=（b₁-b₂）（1-）＜0，
∴∅（b₁）＜∅（b₂），
∴∅（b）在（1，+∞）上为增函数．
∴∅（b）＞∅（1）=2．…（9分）
所以＞1．…（10分）
（3）解：由b=（）²，
得4b=a²+b²+2ab，…（11分）
，
令g（b）=，…（12分）
因为g（3）＜0，g（4）＞0，根据零点存在性定理知，…（13分）
函数g（b）在（3，4）内一定存在零点，
即方程存在3＜b＜4的根．…（14分）
点评：本题考查方程的解的求法，考查不等式的证明，考查零眯存在定理的应用．解题时要认真审题，仔细解答，注意等价转化思想的合理运用．