题目内容
A是由适合以下性质的函数f(x)构成的:对于定义域内任意两个不相等的实数x1,x2,都有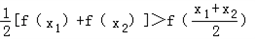 .
.
(1)试判断f(x)=x2及g(x)=log2x是否在集合A中,并说明理由;
(2)设f(x)∈A且定义域为(0,+∞),值域为(0,1),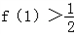 ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.
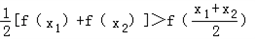 .
.(1)试判断f(x)=x2及g(x)=log2x是否在集合A中,并说明理由;
(2)设f(x)∈A且定义域为(0,+∞),值域为(0,1),
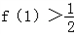 ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.解:(1)f(x)∈A,g(x) A,
A,
对于f(x)∈A的证明.任意x1,x2∈R且x1≠x2
 2,
2,
=
即
∴f(x)∈A
对于g(x) A,举反例:当x1=1,x2=2时,
A,举反例:当x1=1,x2=2时,
 ,
,
 ,
,
不满足 ,
,
∴g(x) A
A
(2)函数 ,当x∈(0,+∞)时,值域为(0,1)且
,当x∈(0,+∞)时,值域为(0,1)且 ,
,
任取x1,x2∈(0,+∞)且x1≠x2,则
=
即 .
.
∴ .是一个符合条件的函数.
.是一个符合条件的函数.
 A,
A,对于f(x)∈A的证明.任意x1,x2∈R且x1≠x2
 2,
2,=

即

∴f(x)∈A
对于g(x)
 A,举反例:当x1=1,x2=2时,
A,举反例:当x1=1,x2=2时, ,
, ,
,不满足
 ,
,∴g(x)
 A
A(2)函数
 ,当x∈(0,+∞)时,值域为(0,1)且
,当x∈(0,+∞)时,值域为(0,1)且 ,
,任取x1,x2∈(0,+∞)且x1≠x2,则

=

即
 .
.∴
 .是一个符合条件的函数.
.是一个符合条件的函数.
练习册系列答案
相关题目