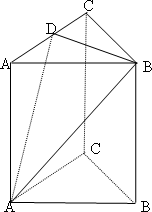
摘要：解: (1)D为A1C1的中点. -------------2分 连结A1B与AB1交于E. 则E为A1B的中点.DE为平面AB1D与平面A1BC1的交线. ∵BC1∥平面AB1D ∴BC1∥DE.∴D为A1C1的中点. -----------6分 (2) 解法一:过D作DF⊥A1B1于F. 由正三棱柱的性质.AA1⊥DF.∴DF⊥平面AB1. 连结EF.DE.在正三角形A1B1C1中. ∵D是A1C1的中点.∴B1D＝A1B1＝a.-------7分 又在直角三角形AA1D中. ∵AD＝＝a.∴AD＝B1D. -------------8分 ∴DE⊥AB1.∴可得EF⊥AB1. 则∠DEF为二面角A1-AB1-D的平面角. -------------10分 可求得DF＝a. ∵△B1FE∽△B1AA1. 得EF＝a.∴∠DEF＝.即为所求. -----12分 建立如图所示空间直角坐标系.则 A(0.-a,0).B1(0.a.a).C1(-a,0.a). A1(0.-a.a).D(-a.-a.a). ∴＝(0.a.a).＝(-a.-a,0). --8分 设＝(x.y.z)是平面AB1D的一个法向量. 则可得.即. ∴＝. ----------10分 又平面AB1的一个法向量 ＝＝(-a,0,0).设n1与n2的夹角是θ. 则 cosθ＝＝. 又可知二面角A1-AB1-D是锐角. ∴二面角A1-AB1-D的大小是.
网址：http://m.1010jiajiao.com/timu_id_4391518[举报]
| |||||||||||
，二面角A－B1D－A1的大小为
，求线段AB的长度．
设数列{an}是公差为d的等差数列，其前n项和为Sn．
（1）已知a1=1，d=2，
（ⅰ）求当n∈N*时，
的最小值；
（ⅱ）当n∈N*时，求证：
+
+…+
＜
；
（2）是否存在实数a1，使得对任意正整数n，关于m的不等式am≥n的最小正整数解为3n-2？若存在，则求a1的取值范围；若不存在，则说明理由． 查看习题详情和答案>>
（1）已知a1=1，d=2，
（ⅰ）求当n∈N*时，
| Sn+64 |
| n |
（ⅱ）当n∈N*时，求证：
| 2 |
| S1S3 |
| 3 |
| S2S4 |
| n+1 |
| SnSn+2 |
| 5 |
| 16 |
（2）是否存在实数a1，使得对任意正整数n，关于m的不等式am≥n的最小正整数解为3n-2？若存在，则求a1的取值范围；若不存在，则说明理由． 查看习题详情和答案>>
已知{an}是公差为d的等差数列，它的前n项和为Sn，等比数列{bn}的前n项和为Tn，S4=2S2+4，b2=
，T2=
（1）求公差d的值；
（2）若对任意的n∈N*，都有Sn≥S8成立，求a1的取值范围
（3）若a1=
，判别方程Sn+Tn=2009是否有解？说明理由．
查看习题详情和答案>>
| 1 |
| 9 |
| 4 |
| 9 |
（1）求公差d的值；
（2）若对任意的n∈N*，都有Sn≥S8成立，求a1的取值范围
（3）若a1=
| 1 |
| 2 |