摘要:(广东)设圆的方程为.直线的方程为的点的坐标为.那么 点在直线上.但不在圆上 点在圆上.但不在直线上 点既在圆上.也在直线上. 点既不在圆上.也不在直线上 (辽宁)已知点..动点.则点的轨迹是 圆 椭圆 双曲线 抛物线
网址:http://m.1010jiajiao.com/timu_id_4389655[举报]
(2012•广东)在平面直角坐标系xOy中,已知椭圆C1:
+
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
 (2013•广东模拟)已知椭圆C1:
(2013•广东模拟)已知椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
(I) 求椭圆C1的方程;
(II) 设点P是抛物线C2:y=x2+h(h∈R)与C1的公共点,C2在点P处的切线与C1交于点另一点M.Q是P关于X轴的对称点,问中否存在h使点Q在以PM为直径的圆上.
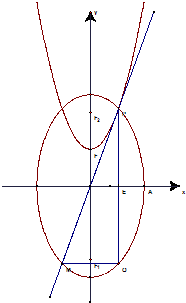
(广东卷理18文20)设![]() ,椭圆方程为
,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() .如图4所示,过点
.如图4所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为![]() ,已知抛物线在点
,已知抛物线在点![]() 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设![]() 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).