题目内容
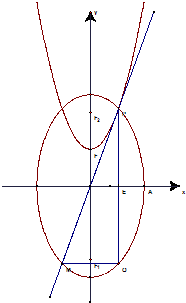 (2013•广东模拟)已知椭圆C1:
(2013•广东模拟)已知椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
(I) 求椭圆C1的方程;
(II) 设点P是抛物线C2:y=x2+h(h∈R)与C1的公共点,C2在点P处的切线与C1交于点另一点M.Q是P关于X轴的对称点,问中否存在h使点Q在以PM为直径的圆上.
分析:(I)利用椭圆C1:
+
=1(a>b>0)的右顶点A(1,0),一个焦点与点A、B构成等边三角形,建立方程,求出几何量,即可求椭圆C1的方程;
(II)假设存在h使点Q在以PM为直径的圆上,利用
•
=0,
∥
,即可求得结论.
| y2 |
| a2 |
| x2 |
| b2 |
(II)假设存在h使点Q在以PM为直径的圆上,利用
| QP |
| QM |
| QM |
| OA |
解答:解:(I)由题意,∵椭圆C1:
+
=1(a>b>0)的右顶点A(1,0),一个焦点与点A、B构成等边三角形
∴b=1,2•
=1
∴a=2,b=1
∴所求的椭圆方程为
+x2=1,
(II)不妨设P(t,t2+h),M(x0,y0),则(t2+h)2+4t2-4=0(1)
假设存在h使点Q在以PM为直径的圆上,则
•
=0
∵
∥
∴M(-t,-t2-h),∴2t=
∴h=t2>0
代入(1)得h2+h-1=0
∴h=
∴存在h=
,使点Q在以PM为直径的圆上.
| y2 |
| a2 |
| x2 |
| b2 |
∴b=1,2•
| b2 |
| a |
∴a=2,b=1
∴所求的椭圆方程为
| y2 |
| 4 |
(II)不妨设P(t,t2+h),M(x0,y0),则(t2+h)2+4t2-4=0(1)
假设存在h使点Q在以PM为直径的圆上,则
| QP |
| QM |
∵
| QM |
| OA |
∴M(-t,-t2-h),∴2t=
| t2+h |
| t |
∴h=t2>0
代入(1)得h2+h-1=0
∴h=
| ||
| 2 |
∴存在h=
| ||
| 2 |
点评:本题考查椭圆的标准方程与椭圆的几何性质,考查向量知识,考查学生的计算能力,求得椭圆的方程是关键.

练习册系列答案
相关题目
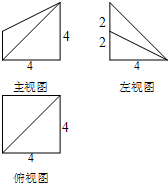 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为