摘要：已积=(2.0).=(2.2).= .则与夹角的范围是( ) A.[0.] B.[.] C.[.] D.[.]
网址：http://m.1010jiajiao.com/timu_id_4385341[举报]
已知向量a=(cosα ，sinα)，b=(cosβ，sinβ)，且a与b之间满足关系：|ka+b|=|a-kb|，其中k>0。
（1）求将a与b的数量积用k表示的解析式f(k)；
（2）a能否和b垂直？a能否和b平行？若不能，则说明理由；若能，则求出对应的k值；
（3）求a与b夹角的最大值。
查看习题详情和答案>>
（1）求将a与b的数量积用k表示的解析式f(k)；
（2）a能否和b垂直？a能否和b平行？若不能，则说明理由；若能，则求出对应的k值；
（3）求a与b夹角的最大值。
已知向量a=(cos a
，sin a
)，b=(cos b
，sin b
)，且a、b满足关系
(k＞0)．
(1)求a与b的数量积用k表示的解析式f(x)．
(2)a能否和b垂直？a能否和b平行？若不能，则说明理由；若能，则求出相应的k值．
(3)求a与b夹角的最大值．
查看习题详情和答案>>已知向量a=(cos a
，sin a
)，b=(cos b
，sin b
)，且a、b满足关系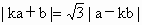
(k＞0)．
(1)求a与b的数量积用k表示的解析式f(x)．
(2)a能否和b垂直？a能否和b平行？若不能，则说明理由；若能，则求出相应的k值．
(3)求a与b夹角的最大值．
查看习题详情和答案>>在同一平面内，已知
=(cosα，sinα)，
=(cosβ，sinβ)，且
•
=0．若
′=(cosα，2sinα)，
′=(cosβ，2sinβ)，则△A'OB'的面积等于（ ）
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．
（1）选修4-2：矩阵与变换
已知点A（1，0），B（2，2），C（3，0），矩阵M表示变换”顺时针旋转45°”．
（Ⅰ）写出矩阵M及其逆矩阵M-1；
（Ⅱ）请写出△ABC在矩阵M-1对应的变换作用下所得△A1B1C1的面积．
（2）选修4-4：坐标系与参数方程
过P（2，0）作倾斜角为α的直线l与曲线E：
（θ为参数）交于A，B两点．
（Ⅰ）求曲线E的普通方程及l的参数方程；
（Ⅱ）求sinα的取值范围．
（3）（选修4-5 不等式证明选讲）
已知正实数a、b、c满足条件a+b+c=3，
（Ⅰ）求证：
+
+
≤3；
（Ⅱ）若c=ab，求c的最大值．
查看习题详情和答案>>
（1）选修4-2：矩阵与变换
已知点A（1，0），B（2，2），C（3，0），矩阵M表示变换”顺时针旋转45°”．
（Ⅰ）写出矩阵M及其逆矩阵M-1；
（Ⅱ）请写出△ABC在矩阵M-1对应的变换作用下所得△A1B1C1的面积．
（2）选修4-4：坐标系与参数方程
过P（2，0）作倾斜角为α的直线l与曲线E：
|
（Ⅰ）求曲线E的普通方程及l的参数方程；
（Ⅱ）求sinα的取值范围．
（3）（选修4-5 不等式证明选讲）
已知正实数a、b、c满足条件a+b+c=3，
（Ⅰ）求证：
| a |
| b |
| c |
（Ⅱ）若c=ab，求c的最大值．