题目内容

已知向量a=(cos a ，sin a )，b=(cos b ，sin b )，且a、b满足关系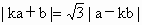(k＞0)．

(1)求a与b的数量积用k表示的解析式f(x)．

(2)a能否和b垂直？a能否和b平行？若不能，则说明理由；若能，则求出相应的k值．

(3)求a与b夹角的最大值．

答案：略
解析：

解：(1)由已知|a|=|b|=1，

∵，

∴，

∴，

∴，

∴．

(2)∵a·b=f(k)＞0，

∴a与b不可能垂直．

若a∥b，由a·b＞0知a、b同向，于是有

a·b=|a||b|cos0=|a||b|=1，

即，解之得．

∴当时，a∥b．

(3)设a与b的夹角为q ，则

，

∴

，

∴当，即k=1时，cosq 取到最小值为．

又0°≤q ≤180°，

∴a与b夹角q 的最大值为60°．


练习册系列答案
相关题目
已知向量
a
=(-cosα，1+sinα)，
b
=(2sin2
α
2
，sinα)．
（Ⅰ）若|
a
+
b
|=
3
，求sin2α的值；
（Ⅱ）设
c
=(cosα，2)，求(
a
+
c
)•
b
的取值范围．
已知向量
a
=(cosωx-sinωx，sinωx)，
b
=(-cosωx-sinωx，2
3
cosωx)，其中ω＞0，且函数f(x)=
a
•
b
+λ（λ为常数）的最小正周期为π．
（Ⅰ）求函数y=f（x）的图象的对称轴；
（Ⅱ）若函数y=f（x）的图象经过点(
π
4
，0)，求函数y=f（x）在区间[0，
5π
12
]上的取值范围．
已知向量
a
=(cos
θ
2
，sin
θ
2
)，
b
=(2，1)，且
a
⊥
b
．
（1）求tanθ的值；
（2 ）求
cos2θ
2
cos(
π
4
+θ)•sinθ
的值．
已知向量
a
=(cos(ωx-
π
6
)，  sin(ωx-
π
4
))，  
b
=(sin(
2
3
π-ωx)， sin(ωx+
π
4
))（其中ω＞0）．若函数f(x)=2
a
•
b
-1的图象相邻对称轴间距离为
π
2
．
（Ⅰ）求ω的值；
（Ⅱ）求f（x）在[-
π
12
，  
π
2
]上的值域．
已知向量
a
=(cosθ，sinθ)，
b=
(cos2θ-1，sin2θ)，
c
=(cos2θ，sin2θ-
3
)．其中θ≠kπ，k∈Z．
（1）求证：
a
⊥
b
；
（2）设f(θ)=
a
•
c
，且θ∈(0，π)，求f(θ)的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网