摘要：23．[解法一](1)由.得. ．．．．．．2分 整理后.可得...为整数. 不存在..使等式成立. ．．．．．．5分 (2)若.即. (*) (ⅰ)若则. 当{}为非零常数列.{}为恒等于1的常数列.满足要求. ．．．．．．7分 (ⅱ)若.(*)式等号左边取极限得.(*)式等号右边的极限只有当时.才能等于1.此时等号左边是常数..矛盾. 综上所述.只有当{}为非零常数列.{}为恒等于1的常数列.满足要求.．．．．．．10分 [解法二]设 则 (i) 若d=0.则 (ii) 若即.则d=0.矛盾 综上所述.有. 10分 (3) 设. . . 13分 取 15分 由二项展开式可得正整数M1.M2.使得(4-1)2s+2=4M1+1, 故当且仅当p=3s,sN时.命题成立. 说明:第(3)题若学生从以下角度解题.可分别得部分分 若p为偶数.则am+1+am+2+--+am+p为偶数.但3k为奇数 故此等式不成立.所以.p一定为奇数. 当p=1时.则am+1=bk,即4m+5=3k. 而3k=(4-1)k = 当k为偶数时.存在m.使4m+5＝3k成立 1分 当p=3时.则am+1+am+2+am+3=bk,即3am+2-bk, 也即3=3k,所以4m+9=3k-1,4(m+1)+5=3k-1 由已证可知.当k-1为偶数即k为奇数时.存在m, 4m+9=3k成立 2分 当p=5时.则am+1+am+2+--+am+5=bk,即5am+3=bk 也即5=3k,而3k不是5的倍数.所以.当p=5时.所要求的m不存在 故不是所有奇数都成立. 2分
网址：http://m.1010jiajiao.com/timu_id_4383210[举报]
已知数列
的前
项和为
，且
(
N*),其中
．
(Ⅰ) 求的通项公式；
(Ⅱ) 设
(
N*).
①证明： 
；
② 求证：
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用
关系式，表示通项公式，然后得到第一问，第二问中利用放缩法得到
，②由于
，
所以
利用放缩法，从此得到结论。
解：(Ⅰ)当
时，由
得
. ……2分
若存在
由
得
，
从而有
，与矛盾，所以
.
从而由得
得
. ……6分
(Ⅱ)①证明：
证法一：∵
∴
∴
∴
.…………10分
证法二：
，下同证法一.
……10分
证法三：（利用对偶式）设
，
，
则
.又
，也即
，所以
，也即
，又因为
，所以
.即
………10分
证法四：（数学归纳法）①当
时, 
,命题成立;
②假设
时,命题成立,即
,
则当
时,
即
即
故当时，命题成立.
综上可知，对一切非零自然数，不等式②成立. ………………10分
②由于，
所以，
从而
.
也即
查看习题详情和答案>>
已知二次函数f（x）=ax2+bx+3是偶函数，且过点（-1，4），函数g（x）=x+4．
（1）求f（x）的解析式；
（2）求函数y=f（2x）+g（2x+1）的值域；
（3）定义在[p，q]上的一个函数m（x），用分法T：p=x0＜x1＜…＜xi-1＜xi＜…＜xn=q将区间[p，q]任意划分成n个小区间，如果存在一个常数M＞0，使得不等式|m（x1）-m（x0）|+|m（x2）-m（x1）|+…+|m（xi）-m（xi-1）|+…+|m（xn）-m（xn-1）|≤M恒成立，则称函数m（x）为在[p，q]上的有界变差函数．试判断函数f（x）是否为在[1，2]上的有界变差函数？若是，求M的最小值；若不是，请说明理由．
查看习题详情和答案>>
（1）求f（x）的解析式；
（2）求函数y=f（2x）+g（2x+1）的值域；
（3）定义在[p，q]上的一个函数m（x），用分法T：p=x0＜x1＜…＜xi-1＜xi＜…＜xn=q将区间[p，q]任意划分成n个小区间，如果存在一个常数M＞0，使得不等式|m（x1）-m（x0）|+|m（x2）-m（x1）|+…+|m（xi）-m（xi-1）|+…+|m（xn）-m（xn-1）|≤M恒成立，则称函数m（x）为在[p，q]上的有界变差函数．试判断函数f（x）是否为在[1，2]上的有界变差函数？若是，求M的最小值；若不是，请说明理由．
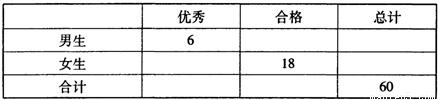
在综合素质评价的某个维度的测评中，依据评分细则，学生之间相互打分，最终将所有的数据合成一个分数．满分100分，按照大于等于80分为优秀，小于80分为合格．为了解学生在该维度的测评结果，从毕业班中随机抽出一个班的数据．该班共有60名学生，得到如下的列联表．
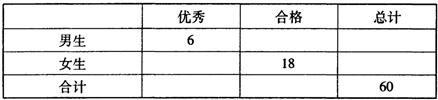
已知在该班随机抽取1人测评结果为优秀的概率为
．
（1）请完成上面的列联表；
（2））能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系？
（3）现在如果想了解全校学生该维度的表现情况，采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析，请你选择一个合适的抽样方法，并解释理由． 查看习题详情和答案>>
已知在该班随机抽取1人测评结果为优秀的概率为
| 1 | 3 |
（1）请完成上面的列联表；
（2））能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系？
（3）现在如果想了解全校学生该维度的表现情况，采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析，请你选择一个合适的抽样方法，并解释理由． 查看习题详情和答案>>
．
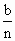元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工，并将最后剩余部分作为公司发展基金．
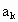(1≤k≤n)为第A位职工所得奖金额，试求
，
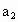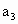，并且用无，n和b表示
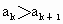(k=l，2，…，n－1)，并解释此不等式关于分配原则的实际意义．