摘要：例1 求函数y＝sinπ的单调增区间 误解:令u＝π ∵y＝sinu在［2kπ-.2kπ+］(k∈Z)上递增 ∴2kπ-≤π≤2kπ+ 解得-4k≤x≤-4k+2 ∴原函数的单调递增区间为［-4k.-4k+2］(k∈Z) 分析:上述解答貌似正确.实则错误.错误的原因是.令u＝π.忽视了u是x的减函数.未考虑复合后单调性的变化 正解如下: 解法一:令u＝π.则u是x的减函数 又∵y＝sinu在［2kπ+.2kπ+］(k∈Z)上为减函数. ∴原函数在［2kπ+.2kπ+］(k∈Z)上递增 设2kπ+≤π≤2kπ+ 解得-4k-2≤x≤-4k(k∈Z) ∴原函数在［-4k-2.-4k］(k∈Z)上单调递增 解法二:将原函数变形为y＝-sinπ 因此只需求sinπ＝y的减区间即可 ∵u＝π为增函数 ∴只需求sinu的递减区间 ∴2kπ+≤π≤2kπ+ 解之得:4k+2≤x≤4k+4(k∈Z) ∴原函数的单调递增区间为［4k+2.4k+4］(k∈Z)
网址：http://m.1010jiajiao.com/timu_id_4382010[举报]
已知定义在区间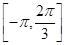
上的函数y＝f(x)的图象关于直线x＝－
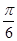对称，当x∈
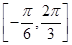时，函数f(x)＝Asin(ωx＋φ) 
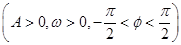的图象如图所示．
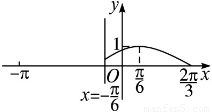
(1)求函数y＝f(x)在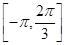上的表达式；
(2)求方程f(x)＝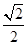
的解．
查看习题详情和答案>>
(2009～2010·浙江嵊泗中学高一期末)已知定义在区间
上的函数y＝f(x)的图象关于直线x＝－
对称，当x∈
时，函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，－
<φ<)的图象如图所示．
(1)求函数y＝f(x)在上的表达式；
(2)求方程f(x)＝
的解．
查看习题详情和答案>>
已知函数f(x)＝ax2－2x＋1，g(x)＝ln(x＋1)．
(1)求函数y＝g(x)－x在[0,1]上的最小值；
(2)当a≥
时，函数t(x)＝f(x)＋g(x)的图像记为曲线C，曲线C在点(0,1)处的切线为l，是否存在a使l与曲线C有且仅有一个公共点？若存在，求出所有a的值；否则，说明理由．
(3)当x≥0时，g(x)≥－f(x)＋恒成立，求a的取值范围．
满足：
记y＝f(x)． 
不等式｜a－lnx｜－ln[f '(x)－3x]＞0恒成立，求实数a的取值范围：
sinx＋1(x∈R).
的最大值，并指出取得最大值时相应的x的值；