摘要：平面向量的坐标表示:在直角坐标系中.分别取与x轴.y轴方向相同的两个单位向量作为基底.由平面向量的基本定理知.该平面内的任一向量可表示成.由于与数对(x,y)是一一对应的.因此把(x,y)叫做向量的坐标.记作=(x,y).其中x叫作在x轴上的坐标.y叫做在y轴上的坐标. (1) 若,则 (2)若A(x1,y1),B(x2,y2)则, 表示相等向量的有向线段的始点.终点的坐标未必相同. (3) 向量相等ó坐标相同.
网址：http://m.1010jiajiao.com/timu_id_4374184[举报]
在平面直角坐标系中，已知向量
=(mx，2(y-2))，
=(x，y+2)（m∈R），且满足
⊥
，动点M（x，y）的轨迹为C．
（Ⅰ）求轨迹C的方程，并说明该方程所表示的轨迹的形状；
（Ⅱ）若已知圆O：x2+y2=1，当m=1时，过点M作圆O的切线，切点为A、B，求向量
•
的最大值和最小值．
查看习题详情和答案>>
| a |
| b |
| a |
| b |
（Ⅰ）求轨迹C的方程，并说明该方程所表示的轨迹的形状；
（Ⅱ）若已知圆O：x2+y2=1，当m=1时，过点M作圆O的切线，切点为A、B，求向量
| OA |
| OB |
在平面直角坐标系中，已知向量
（
），
，动点
的轨迹为T．
（1）求轨迹T的方程,并说明该方程表示的曲线的形状；
（2）当
时，已知
、
，试探究是否存在这样的点
： 是轨迹T内部的整点（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积
？若存在，求出点Q的坐标，若不存在，说明理由．
在平面直角坐标系中，对其中任何一向量
，定义范数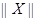
，它满足以下性质：⑴
，当且仅当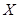
为零向量时，不等式取等号；⑵对任意的实数
， 
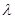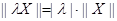（注：此处点乘号为普通的乘号）；⑶
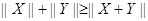．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量
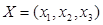，下面给出的几个表达式中，可能表示向量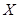的范数的是
（把所有正确答案的序号都填上）
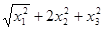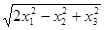⑴
⑵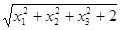 
⑶
⑷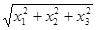
查看习题详情和答案>>
)，b＝(kx，y＋
时，已知点B(0，－
线l：y＝x＋m
，使点B关于直线l的对称点落在轨迹T上？若存在，求出直线l的方程，若不存在，请说明理由.
、
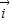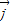为直角坐标平面内x、y轴正方向上的单位向量，若向量
，
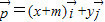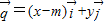，（x，y∈R，m≥2），且
．
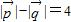x-3与点M的轨迹交于B、C两点，问是否存在实数m，使得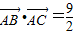
？若存在，求出m的值；若不存在，说明理由．