摘要：1．复数的加.减.乘.除运算按以下法则进行: 设则 (前前减后后.里里加外外)
网址：http://m.1010jiajiao.com/timu_id_4371920[举报]
已知点P(-2
，0)，Q(2
，0)，动点N（x，y），设直线NP，NQ的斜率分别记为k1，k2，记k1?k2=-
（其中“?”可以是四则运算加、减、乘、除中的任意一种运算），坐标原点为O，点M（2，1）．
（Ⅰ）探求动点N的轨迹方程；
（Ⅱ）若“?”表示乘法，动点N的轨迹再加上P，Q两点记为曲线C，直线l平行于直线OM，且与曲线C交于A，B两个不同的点．
（ⅰ）若原点O在以AB为直径的圆的内部，试求出直线l在y轴上的截距m的取值范围．
（ⅱ）试求出△AOB面积的最大值及此时直线l的方程．
查看习题详情和答案>>
| 2 |
| 2 |
| 1 |
| 4 |
（Ⅰ）探求动点N的轨迹方程；
（Ⅱ）若“?”表示乘法，动点N的轨迹再加上P，Q两点记为曲线C，直线l平行于直线OM，且与曲线C交于A，B两个不同的点．
（ⅰ）若原点O在以AB为直径的圆的内部，试求出直线l在y轴上的截距m的取值范围．
（ⅱ）试求出△AOB面积的最大值及此时直线l的方程．
已知点M（k，l）、P（m，n），（klmn≠0）是曲线C上的两点，点M、N关于x轴对称，直线MP、NP分别交x轴于点E（xE，0）和点F（xF，0），
（Ⅰ）用k、l、m、n分别表示xE和xF；
（Ⅱ）当曲线C的方程分别为：x2+y2=R2（R＞0）、
+
=1(a＞b＞0)时，探究xE•xF的值是否与点M、N、P的位置相关；
（Ⅲ）类比（Ⅱ）的探究过程，当曲线C的方程为y2=2px（p＞0）时，探究xE与xF经加、减、乘、除的某一种运算后为定值的一个正确结论． 查看习题详情和答案>>
（Ⅰ）用k、l、m、n分别表示xE和xF；
（Ⅱ）当曲线C的方程分别为：x2+y2=R2（R＞0）、
| x2 |
| a2 |
| y2 |
| b2 |
（Ⅲ）类比（Ⅱ）的探究过程，当曲线C的方程为y2=2px（p＞0）时，探究xE与xF经加、减、乘、除的某一种运算后为定值的一个正确结论． 查看习题详情和答案>>
圆锥曲线上任意两点连成的线段称为弦．若圆锥曲线上的一条弦垂直于其对称轴，我们将该弦称之为曲线的垂轴弦．已知点P（x0，y0）、M（m，n）是圆锥曲线C上不与顶点重合的任意两点，MN是垂直于x轴的一条垂轴弦，直线MP、NP分别交x轴于点E（xE，0）和点F（xF，0）．（1）试用x0，y0，m，n的代数式分别表示xE和xF；
（2）若C的方程为
| x2 |
| a2 |
| y2 |
| b2 |
（3）请选定一条除椭圆外的圆锥曲线C，试探究xE和xF经过某种四则运算（加、减、乘、除），其结果是否是与MN和点P位置无关的定值，写出你的研究结论并证明． 查看习题详情和答案>>
、
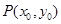是圆锥曲线C
上不与顶点重合的任意两点，
是垂直于
轴的一条垂轴弦，直线
分别交
和点
。
的代数式分别表示
和
；
（如图），求证：
是与
位置无关的定值；
结果是否是与