摘要：如图,求与向量=.-1)和=(1.)夹角相等.且模为的向量的坐标. 法一:设=(x.y).则·=x-y.·=x+y ∵ <.>=<.> ∴ ∴ 即 ① 又||= ∴ x2+y2=2 ② 由①②得 或(舍) ∴= 法二:从分析形的特征着手 ∵ ||=||=2, ·=0 ∴ △AOB为等腰直角三角形.如图 ∵ ||=.∠AOC=∠BOC ∴ C为AB中点 ∴ C()
网址：http://m.1010jiajiao.com/timu_id_4371916[举报]
A、选修4-1：几何证明选讲 如图，PA与⊙O相切于点A，D为PA的中点，
过点D引割线交⊙O于B，C两点，求证：∠DPB=∠DCP．
B．选修4-2：矩阵与变换
已知矩阵M=
|
C．选修4-4：坐标系与参数方程
在极坐标系中，圆C的方程为ρ=2
| 2 |
| π |
| 4 |
|
D．选修4-5：不等式选讲
求函数y=
| 1-x |
| 4+2x |
【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
若多做，则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤.
A． 选修4-1：几何证明选讲
如图，圆
与圆
内切于点
，其半径分别为
与
，
圆的弦
交圆于点
（不在上），
求证：
为定值。
B． 选修4-2：矩阵与变换
已知矩阵
，向量
，求向量
，使得
．
C．选修4-4：坐标系与参数方程
在平面直角坐标系
中，求过椭圆
（
为参数）的右焦点且与直线
（
为参数）平行的直线的普通方程。
D．选修4-5：不等式选讲
解不等式：
查看习题详情和答案>>
，其中向量
,三个向量之间的夹角均为
，点
分别在
上且
，
=4，如图
用向量
表示出来，并求
；
用
表示；
与
所成角的余弦值.
的一个特征值为3，求另一个特征值及其对应的一个特征向量．
，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
（t为参数），判断直线l和圆C的位置关系．
的最大值．
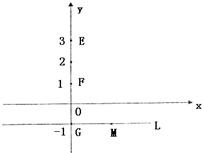如图，O是坐标原点，已知三点E（0，3），F（0，1），G（0，-1），直线L：y=-1，M是直线L上的动点，H．P是坐标平面上的动点，且