题目内容
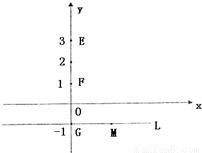
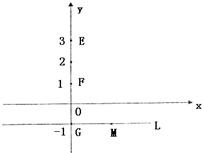 如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且
如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且| FH |
| HM |
| PM |
| EG |
| PH |
| FM |
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)过点E的直线m与点P的轨迹交于相异两点A.B,设向量
| FA |
| FB |
| 3π |
| 4 |
分析:(1)根据且
=
,
=λ
,
•
=0,点P在直线x=a上,由抛物线定义,动点P的轨迹是以F为焦点,直线y=-1为准线的抛物线,求出动点P 轨迹方程;(Ⅱ)直线与抛物线相交,联立方程,利用伟大定理,寻找向量
与
夹角为θ的余弦值,求出直线m斜率的取值范围.
| FH |
| HM |
| PM |
| EG |
| PH |
| FM |
| FA |
| FB |
解答:解:(1)设P(x,y),M(a,0),∵
=λ
,
∴PM∥y轴,
∴点P在直线x=a上.
又|
= |
|,
•
=0,
∴PH⊥FM,点P在线段FM的垂直平分线上,由抛物线定义,动点P的轨迹是以F为焦点,直线y=-1为准线的抛物线,
∴动点P 轨迹方程是x2=4y;
(2) 设A(x1,y1),B(x2,y2),AB的方程:y=kx+3,把它代入x2=4y,得
x2-4kx-12=0,
x1+x2=4k,x1x2=-12,
y1+y2
=4k2-6,y1y2
=9.
设AB在x轴的射影是A1B1,
•
=(x1,y1-1)•(x2,y2-1)=x1x2+y1y2-(y1+y2)+1
|
|•|
|=|FA1|•|FB1|=(y1+1)•(y2+1)=y1y2+(y1+y2)+1,
∴cosθ=
=
≤cos
≤-
,解得|k|≥1+
∴k∈(-∞,-1-
]∪[1+
,+∞)
| PM |
| EG |
∴PM∥y轴,
∴点P在直线x=a上.
又|
| FH| |
| HM |
| PH |
| FM |
∴PH⊥FM,点P在线段FM的垂直平分线上,由抛物线定义,动点P的轨迹是以F为焦点,直线y=-1为准线的抛物线,
∴动点P 轨迹方程是x2=4y;
(2) 设A(x1,y1),B(x2,y2),AB的方程:y=kx+3,把它代入x2=4y,得
x2-4kx-12=0,
x1+x2=4k,x1x2=-12,
y1+y2
| X12+X22 |
| 4 |
| (X1+X2) 2-2X1X2 |
| 4 |
| (X1X2) 2 |
| 16 |
设AB在x轴的射影是A1B1,
| FA |
| FB |
|
| FA |
| FB |
∴cosθ=
| ||||
|
|
| 1-k2 |
| 1+k2 |
| 3π |
| 4 |
| ||
| 2 |
| 2 |
∴k∈(-∞,-1-
| 2 |
| 2 |
点评:考查平面向量与解析几何的结合,体现了向量的工具性,考查了抛物线的定义和直线与抛物线的位置关系,在求解过程中,韦达定理的应用体现了方程的思想,和整体代换的思想方法,属中档题.

练习册系列答案
相关题目
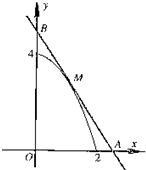 如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.
如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值. (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,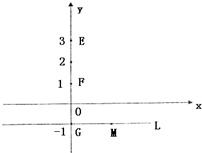 如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且
如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且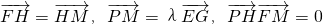 .
.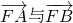 夹角为θ,且
夹角为θ,且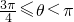 ,求直线m斜率的取值范围.
,求直线m斜率的取值范围.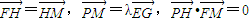 .
.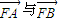 夹角为θ,且
夹角为θ,且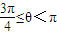 ,求直线m斜率的取值范围.
,求直线m斜率的取值范围.