摘要:7.设f(x)是定义在R上的奇函数.且当x≥0时f(x)=x2.若对任意的x∈[t.t+2]不等式f(x+t)≥2f(x)恒成立.则实数t的取值范围是( ) A.[.+∞) B.[2.+∞) C.(0,2] D.[-.-1]∪[.] 答案:A 解析:当t=时.≤x≤2+.f(x+)-2f(x)=(x+)2-2x2=2+2x-x2≥2+2(2+)2-(2+)2=0.即t=时不等式成立. 当t=2时.2≤x≤4.f(x+2)-2f(x)=(x+2)2-2x2=4+4x-x2≥4+4×4-42>0.∴t=2时不等式成立.所以选A.
网址:http://m.1010jiajiao.com/timu_id_4370043[举报]
设f(x)是定义在R上的奇函数,且f(1+x)=f(1-x),下列说法①f(x+2)=f(x);②f(x+4)=-f(x);③f(1)+f(2)+f(3)+f(4)=0;④f(x+4)=f(x).正确的是( )
A.①②③ B.①③ C.③④ D.②③④
查看习题详情和答案>>设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有![]() 恒成立,则不等式
恒成立,则不等式![]() 的解集是
的解集是
(A) (-2,0) ∪(2,+∞) (B) (-2,0) ∪(0,2) (C) (-∞,-2)∪(2,+∞) (D) (-∞,-2)∪(0,2)
查看习题详情和答案>> 恒成立,则不等式
恒成立,则不等式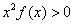 的解集是
的解集是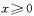 时,
时,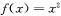 ,若对任意的
,若对任意的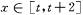 ,不等式
,不等式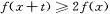 恒成立,则实数t的取值范围是. _______
恒成立,则实数t的取值范围是. _______ 恒成立,则不等式
恒成立,则不等式 的解集是
的解集是