题目内容
设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有
恒成立，则不等式
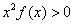的解集是
A．(-2,0) ∪(2,+∞) B．(-2,0) ∪(0,2)
C．(-∞,-2)∪(2,+∞) D．(-∞,-2)∪(0,2)
【答案】
D
【解析】
试题分析：解：因为当x＞0时，有
恒成立，即[
]′＜0恒成立，所以
在（0，+∞）内单调递减．因为f（2）=0，所以在（0，2）内恒有f（x）＞0；在（2，+∞）内恒有f（x）＜0．又因为f（x）是定义在R上的奇函数，所以在（-∞，-2）内恒有f（x）＞0；在（-2，0）内恒有f（x）＜0．又不等式x2f（x）＞0的解集，即不等式f（x）＞0的解集．所以答案为（-∞，-2）∪（0，2）．故选D．
考点：函数单调性与导数
点评：本题主要考查函数求导法则及函数单调性与导数的关系，同时考查了奇偶函数的图象特征
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
]都有f (x1＋x2) = f (x1) ? f (x2)．且f (1) = a＞0．
)；
)，求
．
f(0n)(1-x)n+
f(
)x(1-x)n-1+…+
f(
)xn(1-x)0(x≠0,1).
,又当-3≤x≤-2时，f(x)=2x,则f(113.5)的值是（ ）
B.-
C.
D.-
)x－1，若在区间(－2，6]内关于x的方程f(x)－loga(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是
) D. (