摘要:已知f(x)=. 在内单调递增, 在内单调递减.求a的取值范围. (1)证明 任设x1<x2<-2,则f(x1)-f(x2)= ∵(x1+2)(x2+2)>0,x1-x2<0,∴f(x1)<f(x2),∴f内单调递增. (2)解 任设1<x1<x2,则 f(x1)-f(x2)= ∵a>0,x2-x1>0,∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立. ∴a≤1.综上所述知0<a≤1.
网址:http://m.1010jiajiao.com/timu_id_4357706[举报]
 (x≠a).
(x≠a).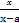 (x≠a).
(x≠a). (x≠a).
(x≠a).