摘要: 函数的对称性. ①满足条件的函数的图象关于直线对称.如已知二次函数满足条件且方程有等根.则= (答:), ②点关于轴的对称点为,函数关于轴的对称曲线方程为, ③点关于轴的对称点为,函数关于轴的对称曲线方程为, ④点关于原点的对称点为,函数关于原点的对称曲线方程为, ⑤点关于直线的对称点为,曲线关于直线的对称曲线的方程为.特别地.点关于直线的对称点为,曲线关于直线的对称曲线的方程为 ,点关于直线的对称点为,曲线关于直线的对称曲线的方程为.如己知函数,若的图像是,它关于直线对称图像是关于原点对称的图像为对应的函数解析式是 (答:), ⑥曲线关于点的对称曲线的方程为.如若函数与的图象关于点对称.则= (答:) ⑦形如的图像是双曲线.其两渐近线分别直线 和直线(由分子.分母中的系数确定).对称中心是点.如已知函数图象与关于直线对称.且图象关于点对称.则a的值为 ⑧的图象先保留原来在轴上方的图象.作出轴下方的图象关于轴的对称图形.然后擦去轴下方的图象得到,的图象先保留在轴右方的图象.擦去轴左方的图象.然后作出轴右方的图象关于轴的对称图形得到.如(1)作出函数及的图象,(2)若函数是定义在R上的奇函数.则函数的图象关于 对称 (答:轴) 提醒:(1)从结论②③④⑤⑥可看出.求对称曲线方程的问题.实质上是利用代入法转化为求点的对称问题,(2)证明函数图像的对称性.即证明图像上任一点关于对称中心的对称点仍在图像上,(3)证明图像与的对称性.需证两方面:①证明上任意点关于对称中心的对称点仍在上,②证明上任意点关于对称中心的对称点仍在上.如(1)已知函数.求证:函数的图像关于点成中心对称图形,(2)设曲线C的方程是,将C沿轴, 轴正方向分别平行移动单位长度后得曲线.①写出曲线的方程(答:),②证明曲线C与关于点对称.
网址:http://m.1010jiajiao.com/timu_id_4357260[举报]
对于两个定义域相同的函数f(x),g(x),若存在实数m,n使h(x)=mf(x)+ng(x),则称函数h(x)是由“基函数f(x),g(x)”生成的。
(1)若f(x)=x2+3x和g(x)=-3x+4生成一个偶函数h(x),求h(2)的值;
(2)若h(x)=2x2+3x-1由函数f(x)=x2+ax,g(x)=x+b(a,b∈R,且ab≠0)生成,求a+2b的取值范围;
(3)试利用“基函数f(x)=log4(4x+1),g(x)=x-1”生成一个函数h(x),使之满足下列条件:
①是偶函数;②有最小值1;求出函数h(x)的解析式并进一步研究该函数的单调性(无需证明)。
查看习题详情和答案>>
(1)若f(x)=x2+3x和g(x)=-3x+4生成一个偶函数h(x),求h(2)的值;
(2)若h(x)=2x2+3x-1由函数f(x)=x2+ax,g(x)=x+b(a,b∈R,且ab≠0)生成,求a+2b的取值范围;
(3)试利用“基函数f(x)=log4(4x+1),g(x)=x-1”生成一个函数h(x),使之满足下列条件:
①是偶函数;②有最小值1;求出函数h(x)的解析式并进一步研究该函数的单调性(无需证明)。
(本题满分12分)
对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内有单调性;②存在区间
在D内有单调性;②存在区间![]() ,使
,使![]() 在区间
在区间![]() 上的值域也为
上的值域也为![]() ,则称
,则称![]() 为D上的闭函数。
为D上的闭函数。
(1)求闭函数![]() 符合条件的区间
符合条件的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由。
是否为闭函数?并说明理由。
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围。
的取值范围。
若函数![]() 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在![]() 使得
使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() ;反之,若
;反之,若![]() 不存在,则称函数
不存在,则称函数![]() 不具有性质
不具有性质![]() 。
。
(1)证明:函数![]() 具有性质
具有性质![]() ,并求出对应的
,并求出对应的![]() 的值;
的值;
(2)已知函数![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围
的取值范围
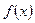 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在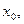 使得
使得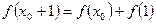 成立,则称函数
成立,则称函数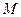 ;反之,若
;反之,若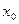 不存在,则称函数
不存在,则称函数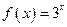 具有性质
具有性质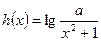 具有性质
具有性质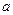 的取值范围
的取值范围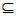 D,使f(x)在区间[a,b]上的值域也为[a,b],则称f(x)为D上的闭函数。
D,使f(x)在区间[a,b]上的值域也为[a,b],则称f(x)为D上的闭函数。 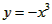 符合条件的区间[a,b];
符合条件的区间[a,b]; 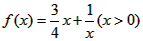 是否为闭函数?并说明理由;
是否为闭函数?并说明理由; 是闭函数,求实数K的取值范围。
是闭函数,求实数K的取值范围。