题目内容
若函数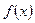 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在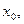 使得
使得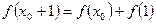 成立,则称函数
成立,则称函数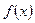 具有性质
具有性质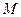 ;反之,若
;反之,若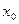 不存在,则称函数
不存在,则称函数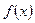 不具有性质
不具有性质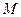 。
。
(1)证明:函数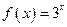 具有性质
具有性质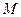 ,并求出对应的
,并求出对应的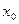 的值;
的值;
(2)已知函数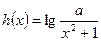 具有性质
具有性质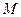 ,求
,求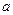 的取值范围
的取值范围
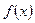 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在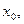 使得
使得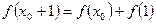 成立,则称函数
成立,则称函数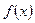 具有性质
具有性质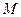 ;反之,若
;反之,若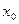 不存在,则称函数
不存在,则称函数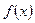 不具有性质
不具有性质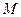 。
。(1)证明:函数
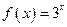 具有性质
具有性质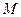 ,并求出对应的
,并求出对应的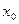 的值;
的值;(2)已知函数
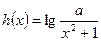 具有性质
具有性质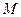 ,求
,求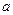 的取值范围
的取值范围(1)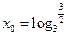 (2)a
(2)a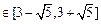
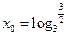 (2)a
(2)a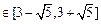
(1)证明: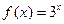 代入
代入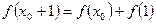 得:
得: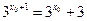 , ……2分
, ……2分
即: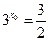 ,解得
,解得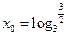 . ……………………………………………5分
. ……………………………………………5分
所以函数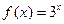 具有性质M.……………………………………………………6分
具有性质M.……………………………………………………6分
(2)解:h(x)的定义域为R,且可得a>0.
因为h(x)具有性质M,所以存在x0,使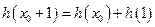 ,
,
代入得: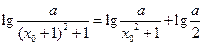 .化为
.化为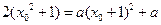 ,
,
整理得: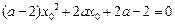 有实根.
有实根.
①若a=2,得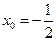 .……………………………………………………………8分
.……………………………………………………………8分
②若a≠2,得△≥0,即a2-6a+4≤0, 解得:a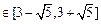 ,
,
所以:a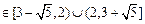 .(若未去掉a=2,扣1分)…………………14分
.(若未去掉a=2,扣1分)…………………14分
综上可得a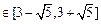 .………………… …………………………………16分
.………………… …………………………………16分
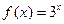 代入
代入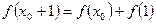 得:
得: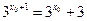 , ……2分
, ……2分即:
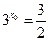 ,解得
,解得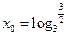 . ……………………………………………5分
. ……………………………………………5分所以函数
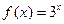 具有性质M.……………………………………………………6分
具有性质M.……………………………………………………6分(2)解:h(x)的定义域为R,且可得a>0.
因为h(x)具有性质M,所以存在x0,使
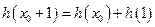 ,
,代入得:
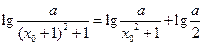 .化为
.化为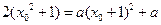 ,
,整理得:
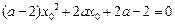 有实根.
有实根. ①若a=2,得
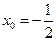 .……………………………………………………………8分
.……………………………………………………………8分②若a≠2,得△≥0,即a2-6a+4≤0, 解得:a
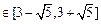 ,
,所以:a
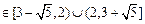 .(若未去掉a=2,扣1分)…………………14分
.(若未去掉a=2,扣1分)…………………14分综上可得a
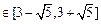 .………………… …………………………………16分
.………………… …………………………………16分
练习册系列答案
相关题目
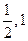 ) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是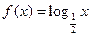 B.
B.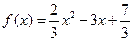
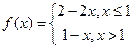 D.
D.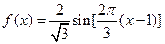
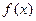 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意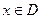 ,等式
,等式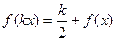 恒成立。(Ⅰ)判断一次函数
恒成立。(Ⅰ)判断一次函数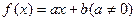 是否属于集合M;(Ⅱ)证明
是否属于集合M;(Ⅱ)证明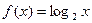 属于集合M,并找到一个常数k;(Ⅲ)已知函数
属于集合M,并找到一个常数k;(Ⅲ)已知函数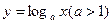 与
与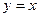 的图像有公共点,试证明
的图像有公共点,试证明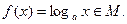
 ,则 ( )
,则 ( )
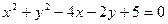 ,则
,则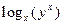 的值是_____________.
的值是_____________.