摘要:函数的奇偶性. (1)具有奇偶性的函数的定义域的特征:定义域必须关于原点对称!为此确定函数的奇偶性时.务必先判定函数定义域是否关于原点对称.如若函数. 为奇函数.其中.则的值是 , (2)确定函数奇偶性的常用方法(若所给函数的解析式较为复杂.应先化简.再判断其奇偶性): ①定义法:如判断函数的奇偶性 . ②利用函数奇偶性定义的等价形式:或().如判断的奇偶性 . ③图像法:奇函数的图象关于原点对称,偶函数的图象关于轴对称. (3)函数奇偶性的性质: ①奇函数在关于原点对称的区间上若有单调性.则其单调性完全相同,偶函数在关于原点对称的区间上若有单调性.则其单调性恰恰相反. ②如果奇函数有反函数.那么其反函数一定还是奇函数. ③若为偶函数.则.如若定义在R上的偶函数在上是减函数.且=2.则不等式的解集为 .(答:) ④若奇函数定义域中含有0.则必有.故是为奇函数的既不充分也不必要条件.如若为奇函数.则实数= . ⑤定义在关于原点对称区间上的任意一个函数.都可表示成“一个奇函数与一个偶函数的和 .如设是定义域为R的任一函数. ..①判断与的奇偶性, ②若将函数.表示成一个奇函数和一个偶函数之和.则= (答:①为偶函数.为奇函数,②=) ⑥复合函数的奇偶性特点是:“内偶则偶.内奇同外 . ⑦既奇又偶函数有无穷多个(.定义域是关于原点对称的任意一个数集).
网址:http://m.1010jiajiao.com/timu_id_4357257[举报]
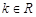 ,函数
,函数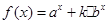
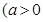 且
且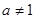 ,
,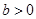 且
且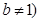 .
. 满足
满足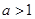 且
且 ,函数
,函数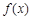 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因;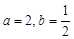 ,讨论函数
,讨论函数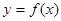 ,定义域为
,定义域为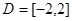 ,以下命题正确的是(只要求写出命题的序号)
,以下命题正确的是(只要求写出命题的序号)
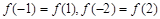 ,则
,则 上的偶函数;
上的偶函数;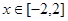 ,都有
,都有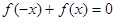 ,则
,则 则
则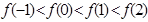 ,则
,则 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有 ,且当
,且当 时,
时, 。
。 是否满足这些条件;
是否满足这些条件; ,求方程
,求方程 的解。
的解。 ,函数
,函数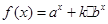
 且
且 ,
, 且
且 .
.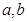 满足
满足 且
且 ,函数
,函数 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因; ,讨论函数
,讨论函数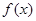 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有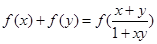 ,且当
,且当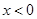 时,
时,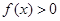 。
。 是否满足这些条件;
是否满足这些条件;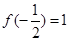 ,求方程
,求方程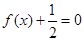 的解。
的解。