题目内容
已知 ,函数
,函数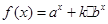
 且
且 ,
, 且
且 .
.
(1) 如果实数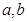 满足
满足 且
且 ,函数
,函数 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因;
(2) 如果 ,讨论函数
,讨论函数 的单调性。
的单调性。
(1) 时,函数
时,函数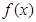 为奇函数;
为奇函数;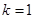 时,函数
时,函数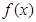 为偶函数.
为偶函数.
(2)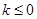 时,
时,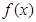 在
在 递增;
递增;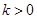 时,减区间
时,减区间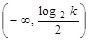 ,增区间
,增区间 .
.
解析试题分析:(1)因为 ,所以
,所以 ,
,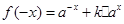 ,根据奇函数偶函数的定义即可求得k的值.(2)
,根据奇函数偶函数的定义即可求得k的值.(2) ,所以
,所以 ,
,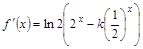 .根据导数的符号即可得函数的单调性.在本题中,由于含有参数k,故需要对k进行讨论.
.根据导数的符号即可得函数的单调性.在本题中,由于含有参数k,故需要对k进行讨论.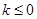 时,
时,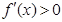 恒成立,
恒成立,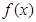 在
在 递增;
递增;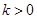 时,若
时,若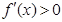 ,则
,则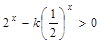 ,
,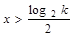 ; 若
; 若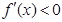 ,则
,则 ,
,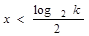 ,增区间
,增区间 ,减区间
,减区间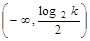 .
.
试题解析:(1)由题意得: ,
,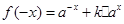 ,
,
若函数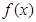 为奇函数,则
为奇函数,则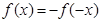 ,
, ;
;
若函数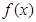 为偶函数,则
为偶函数,则 ,
,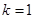 . 6分
. 6分
(2)由题意知: ,
,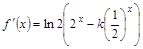 ..7分
..7分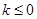 时,
时,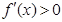 恒成立,
恒成立,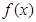 在
在 递增; 9分
递增; 9分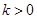 时,若
时,若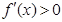 ,则
,则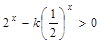 ,
,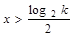
若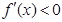 ,则
,则 ,
,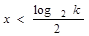
增区间 ,减区间
,减区间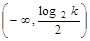 12分
12分
综上: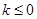 时,
时, 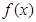 在
在 递增;
递增;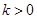 时,减区间
时,减区间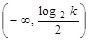 ,增区间
,增区间 . 13分
. 13分
考点:1、函数的奇偶性;2、导数的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 .
. 为偶函数,求
为偶函数,求 的值;
的值; ,求函数
,求函数 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 ,x∈[1,3],
,x∈[1,3], 于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围. .
.
 的图像;
的图像;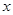 的方程
的方程 在区间
在区间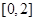 上解的个数.
上解的个数. 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有 (
( ,
,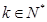 )成立,则称
)成立,则称 阶缩放函数.
阶缩放函数. 时,
时, ,求
,求 的值;
的值; ,求证:函数
,求证:函数 在
在 上无零点;
上无零点; 时,
时, ,求
,求 (
( )上的取值范围.
)上的取值范围.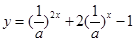 (
( )在
)在 上的最大值为23,求a的值.
上的最大值为23,求a的值. 上的函数
上的函数 当
当 时,
时, ,且对任意的
,且对任意的 有
有 。
。 ,
, ,恒有
,恒有 ;
; ,求
,求 的取值范围。
的取值范围。
 在
在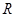 上单调递增;
上单调递增; 的值;
的值; ,求
,求 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
. 表达式;
表达式; 与函数
与函数 的取值范围;
的取值范围;  满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 上.(不要求过程)
上.(不要求过程)