摘要:23.已知椭圆C:=1()的离心率为.短轴一个端点到右焦点的距离为. (1)求椭圆的方程, (2)设直线与椭圆交于.两点.坐标原点到直线的距离为.求△面积的最大值. 昆明三中.滇池中学2010--2011学年上学期期中考试
网址:http://m.1010jiajiao.com/timu_id_4355071[举报]
已知椭圆C: =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,直线
,直线 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(I)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点N( ,-l).
,-l).
查看习题详情和答案>>
 =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,直线
,直线 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.(I)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点N(
 ,-l).
,-l).查看习题详情和答案>>
已知椭圆C: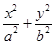 =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线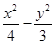 =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin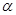 ·x+cos
·x+cos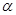 ·y-l=0相切(
·y-l=0相切(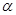 为常数).
为常数).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线与椭圆C相交TA,B两点,设P为椭圆上一点,且满足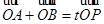 (O为坐标原点),当
(O为坐标原点),当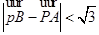 时,求实数t取值范围.
时,求实数t取值范围.
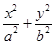 =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线 =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin ·x+cos
·x+cos (O为坐标原点),当
(O为坐标原点),当 时,求实数t取值范围.
时,求实数t取值范围. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+ =0相切.
=0相切. (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|<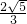 时,求实数t取值范围.
时,求实数t取值范围.