题目内容
已知椭圆C：
=1（a＞b＞0）的离心率
，直线
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切．（I）求椭圆C的方程；
（Ⅱ）设M是椭圆的上顶点，过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1+k2=4，证明：直线AB过定点N（
，-l）．
【答案】分析：（I）由离心率为
得
，由直线l与圆相切得
=b，再由b2+c2=a2即可解得a，b值；
（Ⅱ）要证明直线AB过定点N（
，-l），可证
．设MA：y=k1x+1，代入椭圆方程消掉y得x的二次方程，由韦达定理可表示点A坐标，同理可得点B坐标，由向量共线的条件可证
；
解答：解：（I）由已知得：
，解得
，
故椭圆方程为：
；
（Ⅱ）由（I）知M（0，1），设MA：y=k1x+1，
由
得：
，
则
，所以
，
所以A（-
，
），同理可得B（-
，
），
所以
=（
，
），
，
所以
•
-
=
=
=0，
故
，所以A、B、N三点共线，即直线AB过定点N（-
，-1）．
点评：本题考查椭圆方程、直线方程及其位置关系，考查向量在解析几何中的应用，考查学生对问题的分析转化能力，考查转化思想．
得，由直线l与圆相切得=b，再由b2+c2=a2即可解得a，b值；（Ⅱ）要证明直线AB过定点N（
，-l），可证．设MA：y=k1x+1，代入椭圆方程消掉y得x的二次方程，由韦达定理可表示点A坐标，同理可得点B坐标，由向量共线的条件可证；解答：解：（I）由已知得：
，解得，故椭圆方程为：
；（Ⅱ）由（I）知M（0，1），设MA：y=k1x+1，
由
得：，则
，所以，所以A（-
，），同理可得B（-，），所以
=（，），，所以
•-===0，故
，所以A、B、N三点共线，即直线AB过定点N（-，-1）．点评：本题考查椭圆方程、直线方程及其位置关系，考查向量在解析几何中的应用，考查学生对问题的分析转化能力，考查转化思想．
练习册系列答案
相关题目
+
=1（a＞b＞0）经过（1，1）与（
，
）两点．
+
+
为定值．
已知椭圆C：
+
=1（a＞b＞0）的左右焦点为F1，F2，过F2线与圆x2+y2=b2相切于点A，并与椭圆C交与不同的两点P，Q，如图，PF1⊥PQ，若A为线段PQ的靠近P的三等分点，则椭圆的离心率为（ ）
+
=1（a＞b＞0），直线l为圆O：x2+y2=b2的一条切线，记椭圆C的离心率为e．
，且恰好经过椭圆的右顶点，求e的大小；
y+3=0相切，求椭圆方程．
+
=1（a＞b＞0），直线l为圆O：x2+y2=b2的一条切线，记椭圆C的离心率为e．
，且恰好经过椭圆的右顶点，求e的大小；
y+3=0相切，求椭圆方程．
=1（a>b>0）的离心率为
，且在x轴上的顶点分别为
：
与
轴交于点T，P为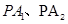
分别与椭圆交于M、N两点，试问直线MN是否通过椭圆的焦点？并证明你的结论.