题目内容
已知椭圆C: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+ =0相切.
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,设P为椭圆上一点,且满足 (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|<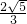 时,求实数t取值范围.
时,求实数t取值范围.
解:(Ⅰ)由题意知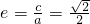 ,所以
,所以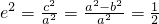 .
.
即a2=2b2.(2分)
又因为 ,所以a2=2,
,所以a2=2, .
.
故椭圆C的方程为 .(4分)
.(4分)
(Ⅱ)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由 得(1+2k2)x2-8k2x+8k2-2=0.△=64k4-4(2k2+1)(8k2-2)>0,
得(1+2k2)x2-8k2x+8k2-2=0.△=64k4-4(2k2+1)(8k2-2)>0, .(6分)
.(6分)
 ,
, ∵
∵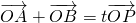 ∴(x1+x2,y1+y2)=t(x,y),
∴(x1+x2,y1+y2)=t(x,y),
∴ ,
,
∵点P在椭圆上,∴ ,∴16k2=t2(1+2k2).(8分)
,∴16k2=t2(1+2k2).(8分)
∵ <
<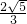 ,∴
,∴ ,∴
,∴
∴ ,∴(4k2-1)(14k2+13)>0,∴
,∴(4k2-1)(14k2+13)>0,∴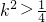 .(10分)
.(10分)
∴ ,∵16k2=t2(1+2k2),∴
,∵16k2=t2(1+2k2),∴ ,
,
∴ 或
或 ,∴实数t取值范围为
,∴实数t取值范围为 .(12分)
.(12分)
分析:(Ⅰ)由题意知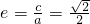 ,所以
,所以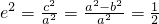 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.
(Ⅱ)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由 得(1+2k2)x2-8k2x+8k2-2=0再由根的判别式和嘏达定理进行求解.
得(1+2k2)x2-8k2x+8k2-2=0再由根的判别式和嘏达定理进行求解.
点评:本题考查椭圆方程的求法和求实数t取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用根的判别式和韦达定理进行解题.
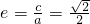 ,所以
,所以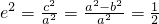 .
.即a2=2b2.(2分)
又因为
 ,所以a2=2,
,所以a2=2, .
.故椭圆C的方程为
 .(4分)
.(4分)(Ⅱ)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),
由
 得(1+2k2)x2-8k2x+8k2-2=0.△=64k4-4(2k2+1)(8k2-2)>0,
得(1+2k2)x2-8k2x+8k2-2=0.△=64k4-4(2k2+1)(8k2-2)>0, .(6分)
.(6分) ,
, ∵
∵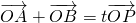 ∴(x1+x2,y1+y2)=t(x,y),
∴(x1+x2,y1+y2)=t(x,y),∴
 ,
,
∵点P在椭圆上,∴
 ,∴16k2=t2(1+2k2).(8分)
,∴16k2=t2(1+2k2).(8分)∵
 <
<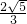 ,∴
,∴ ,∴
,∴
∴
 ,∴(4k2-1)(14k2+13)>0,∴
,∴(4k2-1)(14k2+13)>0,∴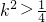 .(10分)
.(10分)∴
 ,∵16k2=t2(1+2k2),∴
,∵16k2=t2(1+2k2),∴ ,
,∴
 或
或 ,∴实数t取值范围为
,∴实数t取值范围为 .(12分)
.(12分)分析:(Ⅰ)由题意知
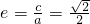 ,所以
,所以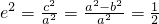 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.(Ⅱ)由题意知直线AB的斜率存在.设AB:y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由
 得(1+2k2)x2-8k2x+8k2-2=0再由根的判别式和嘏达定理进行求解.
得(1+2k2)x2-8k2x+8k2-2=0再由根的判别式和嘏达定理进行求解.点评:本题考查椭圆方程的求法和求实数t取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用根的判别式和韦达定理进行解题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为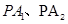 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.