摘要: 解:(1)如图.过点B作BD⊥OA于点D. 在Rt△ABD中. ∵∣AB∣=,sin∠OAB=, ∴∣BD∣=∣AB∣·sin∠OAB =×=3. 又由勾股定理.得 ∴∣OD∣=∣OA∣-∣AD∣=10-6=4. ∵点B在第一象限.∴点B的坐标为(4.3). --3分 设经过O三点的抛物线的函数表达式为 y=ax2+bx. 由 ∴经过O.C.A三点的抛物线的函数表达式为 --2分 中的抛物线上存在点P.使以P.O.C.A为顶点的四边形为梯形 ①∵点C不是抛物线的顶点. ∴过点C做直线OA的平行线与抛物线交于点P1 . 则直线CP1的函数表达式为y=-3. 对于.令y=-3x=4或x=6. ∴ 而点C.∴P1. 在四边形P1AOC中.CP1∥OA,显然∣CP1∣≠∣OA∣. ∴点P1是符合要求的点. --1分 ②若AP2∥CO.设直线CO的函数表达式为 将点C代入.得 ∴直线CO的函数表达式为 于是可设直线AP2的函数表达式为 将点A代入.得 ∴直线AP2的函数表达式为 由.即=0. ∴ 而点A.∴P2. 过点P2作P2E⊥x轴于点E.则∣P2E∣=12. 在Rt△AP2E中.由勾股定理.得 而∣CO∣=∣OB∣=5. ∴在四边形P2OCA中.AP2∥CO,但∣AP2∣≠∣CO∣. ∴点P2是符合要求的点. --1分 ③若OP3∥CA,设直线CA的函数表达式为y=k2x+b2 将点A代入.得 ∴直线CA的函数表达式为 ∴直线OP3的函数表达式为 由即x=0. ∴ 而点O(0,0),∴P3. 过点P3作P3E⊥x轴于点E.则∣P3E∣=7. 在Rt△OP3E中.由勾股定理.得 而∣CA∣=∣AB∣=. ∴在四边形P3OCA中.OP3∥CA,但∣OP3∣≠∣CA∣. ∴点P3是符合要求的点. --1分 综上可知.在(1)中的抛物线上存在点P1.P2.P3, 使以P.O.C.A为顶点的四边形为梯形. --1分 (3)由题知.抛物线的开口可能向上.也可能向下. ①当抛物线开口向上时.则此抛物线与y轴的副半轴交与点N. 可设抛物线的函数表达式为. 即 如图.过点M作MG⊥x轴于点G. ∵Q.G(.N(0.-10ak2).M ∴ ∴ --2分 ②当抛物线开口向下时.则此抛物线与y轴的正半轴交于点N. 同理.可得 --1分 综上所知.的值为3:20. --1分
网址:http://m.1010jiajiao.com/timu_id_4332092[举报]
如图,过点P(2,2
)作x轴的平行线交y轴于点A,交双曲线y=
(x>0)于点N,作PM⊥AN交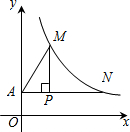 双曲线y=
双曲线y=
(x>0)于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式
≥ax+b的解集.
查看习题详情和答案>>
| 2 |
| k |
| x |
 双曲线y=
双曲线y=| k |
| x |
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式
| k |
| x |
阅读下面的材料,并回答所提出的问题:如图所示,在锐角三角形ABC中,求证:
=
这个三角形不是一个直角三角形,不能直接使用锐角三角函数的知识去处理,所以必须构造直角三角形,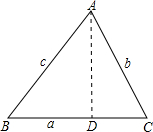 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,sinB=
,则AD=csinB
Rt△ACD中,sinC=
,则AD=bsinC
所以c sinB=b sinC,即
=
(1)在上述分析证明过程中,主要用到了下列三种数学思想方法的哪一种( )
A、数形结合的思想;B、转化的思想;C、分类的思想
(2)用上述思想方法解答下面问题.
在△ABC中,∠C=60°,AC=6,BC=8,求AB和△ABC的面积.
(3)用上述结论解答下面的问题(不必添加辅助线)
在锐角三角形ABC中,AC=10,AB=5
,∠C=60°,求∠B的度数.
查看习题详情和答案>>
| b |
| sinB |
| c |
| sinC |
这个三角形不是一个直角三角形,不能直接使用锐角三角函数的知识去处理,所以必须构造直角三角形,
 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,sinB=
| AD |
| AB |
Rt△ACD中,sinC=
| AD |
| AC |
所以c sinB=b sinC,即
| b |
| sinB |
| c |
| sinC |
(1)在上述分析证明过程中,主要用到了下列三种数学思想方法的哪一种( )
A、数形结合的思想;B、转化的思想;C、分类的思想
(2)用上述思想方法解答下面问题.
在△ABC中,∠C=60°,AC=6,BC=8,求AB和△ABC的面积.
(3)用上述结论解答下面的问题(不必添加辅助线)
在锐角三角形ABC中,AC=10,AB=5
| 6 |
 如图,过A点的一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点B,则不等式0<2x<kx+b的解集是( )
如图,过A点的一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点B,则不等式0<2x<kx+b的解集是( ) 如图,过A点的一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点B,则不等式0<2x<kx+b的解集是
如图,过A点的一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点B,则不等式0<2x<kx+b的解集是