题目内容
如图,过点P(2,2| 2 |
| k |
| x |
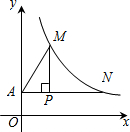 双曲线y=
双曲线y=| k |
| x |
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式
| k |
| x |
分析:(1)首先根据点P(2,2
)的坐标求出N点的坐标,代入反比例函数解析式即可求出;
(2)利用图形两函数谁在上上面谁大,交点坐标即是函数大小的分界点,可以直接判断出函数的大小关系.
| 2 |
(2)利用图形两函数谁在上上面谁大,交点坐标即是函数大小的分界点,可以直接判断出函数的大小关系.
解答: 解:(1)依题意,则AN=4+2=6,
解:(1)依题意,则AN=4+2=6,
∴N(6,
),
把N(6,
)代入y=
得:
xy=6
,
∴k=6
;
(2)∵M点横坐标为2,
∴M点纵坐标为
=3
,
∴M(2,3
),
∴由图象知,
≥ax+b的解集为:
0<x≤2或x≥6.
 解:(1)依题意,则AN=4+2=6,
解:(1)依题意,则AN=4+2=6,∴N(6,
| 2 |
把N(6,
| 2 |
| k |
| x |
xy=6
| 2 |
∴k=6
| 2 |
(2)∵M点横坐标为2,

∴M点纵坐标为
6
| ||
| 2 |
| 2 |
∴M(2,3
| 2 |
∴由图象知,
| k |
| x |
0<x≤2或x≥6.
点评:此题主要考查了反比例函数的性质以及待定系数法求解析式和利用图形判断函数的大小关系,数形结合解决比较函数的大小关系是初中阶段的难点问题,同学们重点学习.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,过点O、A(1,0)、B(0,
如图,过点O、A(1,0)、B(0,| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
 8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
 如图,过点P(2,
如图,过点P(2, 如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例
如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例