摘要:(辽宁省沈阳二中2008-2009学年上学期高三期中考试) 直线恒过定点C.圆C是以点C为圆心.以4为半径的圆. (1)求圆C的方程, (2)设圆M的方程为上任意一点P分别作圆C的两条切线PE.PF.切点为E.F.求的最大值和最小值. [解析](1). (2)设则 在. 由圆的几何性质得 .由此可得 的最大值为-最小值为-8 [点评]向量与解析几何结合是高考命题的重要趋势.本题难度不大.但是如果不能将“向量语言 准确转化为“函数语言 .或在解题中不细心都可能会出现错误.切记:“细节决定成败
网址:http://m.1010jiajiao.com/timu_id_4327726[举报]
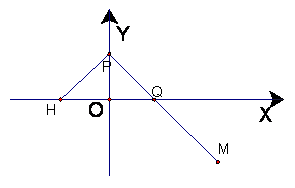
(08年沈阳二中四模文) 已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,试问在
两点,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 成立;
成立;

查看习题详情和答案>>
(08年沈阳二中四模文) 某小组有男生、女生若干人,如果从中选一人参加某项测试,女生被选中的概率是![]() ;如果从中选两人参加测试,两人都是女生的概率为
;如果从中选两人参加测试,两人都是女生的概率为![]() (每个人被选中是等可能的)。
(每个人被选中是等可能的)。
(Ⅰ)求该小组男生、女生各多少人?
(Ⅱ)从该小组选出3人,求男女生都有的概率;
(Ⅲ)若对该小组的同学进行某项测试,其中女生通过的概率为![]() ,男生通过的概率为
,男生通过的概率为![]() ,现对该小组中男生甲、乙和女生丙三人进行测试,求至少有两人通过测试的概率
,现对该小组中男生甲、乙和女生丙三人进行测试,求至少有两人通过测试的概率